実用的に使用される多くの工業材料は粉体である。その粉体の粒子を測定するのが、粒子分析装置である。
では、本装置が、粒子分析機器を他の分析法と比較した場合の特徴は何であろうか?それは、目的とされる測定項目が、主には「大きさ」「形状値」などという「物理的な次元を持った数値」を求める点にある。
他の機器分析法、たとえば、分光光度計などを例にとり比較する。分光光度法を用いて、何かの物質の「濃度」などの物理量を算出するためには、基本的には換算するための「検量線」を必要とする。
しかし、粒子分析機器は検量線を必要とせず、試料を分析装置に投入するだけで粒子径など「大きさ」という物理次元を持った一定の数値を算出する。この際に問題になるのは、
たとえば「粒子径」という数値を算出する目的に作られた装置で同じ試料を測定した値が、必ずしも「同じ値」を示さない場合があるという点である。
このため・・・・・・
※続きをご覧になりたい方は、WEB会員登録後、ログインしていただくことでご覧いただけます。
実用的に使用される多くの工業材料は粉体である。その粉体の粒子を測定するのが、粒子分析装置である。
では、本装置が、粒子分析機器を他の分析法と比較した場合の特徴は何であろうか?それは、目的とされる測定項目が、主には「大きさ」「形状値」などという「物理的な次元を持った数値」を求める点にある。
他の機器分析法、たとえば、分光光度計などを例にとり比較する。分光光度法を用いて、何かの物質の「濃度」などの物理量を算出するためには、基本的には換算するための「検量線」を必要とする。
しかし、粒子分析機器は検量線を必要とせず、試料を分析装置に投入するだけで粒子径など「大きさ」という物理次元を持った一定の数値を算出する。この際に問題になるのは、
たとえば「粒子径」という数値を算出する目的に作られた装置で同じ試料を測定した値が、必ずしも「同じ値」を示さない場合があるという点である。
このため、粒子評価への理解があまり行き届いていないような現場の場合大きな問題になりうる。
また、別の視点で見れば、装置の発展に伴い誰でも簡便に測定できるようになり、測定原理等を理解していなくても装置が使えてしまうという、所謂、分析装置の「ブラックボックス化」や、アプリケーション事例がインターネットなどで容易に手に入ることより、分析目的を深く考えないまま、分析メソッドを構築することなどとも無関係ではないと考える。
この問題を理解するために、何故、「粒子を測定する必要があるのか?」という根本の目的と、粒子分析に関して考える必要がある。
この課題を考えるために、一つの示唆を与える提言として、投影面積円相当径、俗にHeywood 径の提案者で知られるH.Heywood 教授が1st Particle Size Anal. Conf., 1966,にて述べられたとされる以下の文言がある。
“…However, it must be realized that particle size analysis is not an objective in itself but is a means to an end, the end being the correlation of powder properties with some process of manufacture, usage or preparation…
(…しかしながら、粒径測定とはそれ自体は目的ではなく、目的達成のための手段であり、その「目的」は、粉体特性と製造工程もしくは使用工程、前処理工程との相関関係であると認識されるべきである。…)”
粉体とは、主には固形成分である粒子と流体媒体(空気や液体など)の不均一系の複合体を示し非常に多変量の因子が絡み合った、複雑な挙動を示す巨視的(バルク)材料である。
一方、粒子とは、粉体の大部分を構成する重要な微視的な成分であるが、あくまで粉体を構成する1成分である。
上記述べたように、両者の位置づけは明確であり、いくら粒子を厳密に測定しても、目的である粉体特性や最終製品のなどの諸物性のすべてを直接的に理解し、記述することは困難であることを意味する。
すなわち、粒子を測定することにより可能となるのは、目的とする粉体のバルク特性に関する「相関関係に基づく予測」である。
したがって、目的に合わせて、必要とされる粒子径やその分析法を選択する必要があり、どのような分析法や前処理で測定された数値であるか理解する必要がある。
逆に目的と合致しない分析法を選択し、いくら精密に測定しても、評価したい目的を達成できない可能性があるので、その点を留意する必要がある。
粉体のバルク特性と、それに関連する粒子特性との関係性のうち、経験則に基づいた一般的なものを表 1にまとめた。
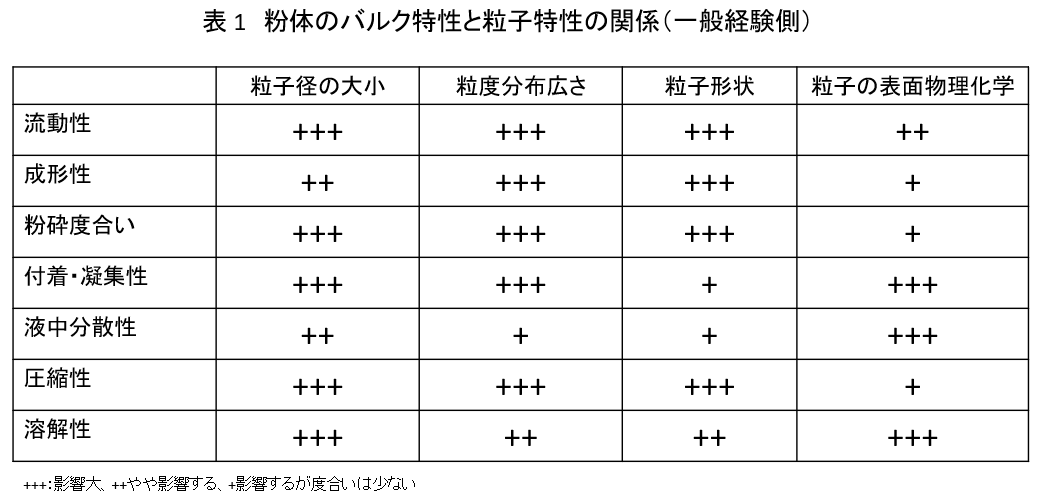
このように、粉体の特性を予測する特性値として使用されるのが、粒子特性の位置づけとなる。種々ある粒子の特性のなかで、
本稿では、形態(Morphology: 径・形状・観察)に着目し、得られた結果の定義、使い方、そして、測定法や試料に対する適用分類に着目して解説する。
粒子径(Particle diameter)とは、粒子の形態情報の中で、粒子の大きさ(粒度;Particle Size)を何らかの方法で定義した一次元の数値、すなわち「長さ」の次元で表現したものである。
粒度は、粉体の主物性の中で最も重要な特性値である。この粒子の径を定義する際、付きまとう問題が、粒子は3次元的な形状を持ち、同一の大きさではない点である。
粒子の形状が全て同じ形状、すなわち、球、円錐、円柱、立方体などの規則的な形状であれば、代表径を規定するのは容易である。
ところが、実際の粉体は一般に複雑な形状を有する粒子で形成されている為、不規則形状の粒子の大きさを定義するためには粒子径の適切な定義を必要とする。
粒子径を定義する際、一般的に用いられるのは、何らかの方法で評価した粒子を円・球として取扱う「円・球相当径」という考え方である1)2)。
幾何学的、物理的にも円や球は最も扱いやすいため、実用上よく用いられ、今日において、工業材料一般での粒子径といえば、円・球相当径で示されていることが多い。また、その他しては最大径・外接・内接長・周囲長などを基準にした多くの定義径がある。
この「粒子径の定義」についてもっとも気をつけるべきことは、「どの粒子径が正しいか」、という議論である。結論から言えば、どの粒子径も正しい。
なぜならば、粒子径とは必要とされる指標・目的に応じて、定義づけされるべきものだからであるである。
ここで例として、1辺を1mmとする立方体粒子について、表面積と体積球相当粒子径を考える。この場合、体積は1mm3であり、表面積は6mm2となる。ここから、球の体積、表面積をそれぞれ、V=4/3πrv3、S=4πrs2として代入して逆算し、直径(2r)として換算すると、2rv≒1.24mm、2rs≒1.38mmとなる。両者の差は0.14mmであるので、体積定義径を基準にすると0.14/1.24(mm)で10%前後もの数値差異が生じる。
このように、おなじ粒子であっても、その定義径により差異が生じるため、その目的に応じた粒子径を適切に選択し、理解しつつ評価する必要がある。
粒子径が物性に与える影響は種々あるが、よく知られている例として、薬物の薬効へ大きく影響する溶解性がある。
薬物の液中における溶解速度を議論する際、よく用いられるモデル式でNernst-Noyes-Whitney式がある。この式は、下記式定義される。
dC/dt=kS(Cs-C)
溶解速度はdC/dt、kは溶解速度定数、Sは表面積、Csは溶解度、Cは時刻tにおける濃度で定義される。
上記式から明らかのように、この場合、表面積Sが大きくなると溶解速度が速くなる。
この式に従い、癲癇薬として用いられる難溶性薬物であるフェニトインを4μm程度に小粒子化することで、薬物の模擬体液への溶出性の改善と、実際の血中濃度放出速度、滞在時間が向上した、という新熊らの研究1) がよく知られている。
このように、時に各種物性に著しい影響を及ぼす粒子径は非常に重要である。
一般に取り扱われる粒子においては、指標に決定された粒子径はばらつきを持ち、同じ大きさの粒子で形成されているものは非常に稀である。
世の中にあるものの「ばらつき(=分布)」の度合いは「分布関数」で表現できる。粒子径を分布関数として取り扱ったものを「粒度分布(Particle size distribution ; PSD)」と呼ぶ。
一般に統計的な分布を表現されるのに用いられるのは「正規分布(Gaussian)」である。
しかし、粒度分布においては、主に対数正規分布で取り扱われる場合が多い。この理由は主に2つである。
第一に、「正規分布は平均値が0になり、かつ、負の値も取りうる」という数学的な原則によるものである。
正規分布を自然界に対して取り扱うならば、粒子径は負値もとる必要がある。しかし、粒子径は物理的に負値を取りえない。
したがって、数学的に粒子径の取り扱いに、正規分布を用いることは適切ではない。
第二に、粉体中の粒子の大きさは、一般的な製造工程(粉砕など)を経た場合、粗い粒子側から細粒部に対して長い裾をひき、粒子径が無限小に収束する非対称分布になる。
特に粉砕工程などではこの傾向が顕著になる。
この理由を単純なモデルで説明する。1個の粒子を正確に2つに砕く工程を考える。
この場合、1回の粉砕操作で粉砕操作のn回数だけ、粒子は2n個に分割されていくことになる。
このため、粒子の個数は指数関数的に増えていくことで、その個数頻度は細かい粒子側に個数が非対称に分布することになる。その結果、粒子径の分布は非対称性の高いデータを取り扱うことになり、対数軸が表現に適していることになる。
粒度分布の取り扱いには主に個数基準と体積基準がある。個数基準の粒子径は、粒子個数を基準にしており、すべての粒子を同等に扱う。
したがって、微粉も粗粉も同等に1つの粒子として計算するため、微粉の検出には向く。
一方、体積基準粒子径は、体積を基準にしているため、計算される量は、径の三乗に比例して大きくなる。
したがって、粗大粒子の検出に向いている。これらのことを簡単な例で説明する。たとえば、1μmの粒子と100μmの粒子を考える。
体積基準で考えた場合、1μm径の微粉、100万個の粒子数で100μmの体積をもつ粒子と同等の体積となる。
しかし、その個数はわずか100万分の1である。したがって、微粉を管理するためには、体積基準のみでは困難であり、逆に粗大の検出は、より体積基準が適している。
このように、目的に応じて適切に基準は選択されるべきである。
大きさや形にばらつきのある粒子を表現するための統計分布である粒度分布は、主には頻度分布と積算分布で示される。
頻度分布とは、各粒子径に対する体積や個数の頻度を示す。
積算分布とは最大径より小さい粒子が粉体全体に占める量的割合を示す。
それらの分布から様々な数値化をなされる場合が多い。その例を図.1.に示した。
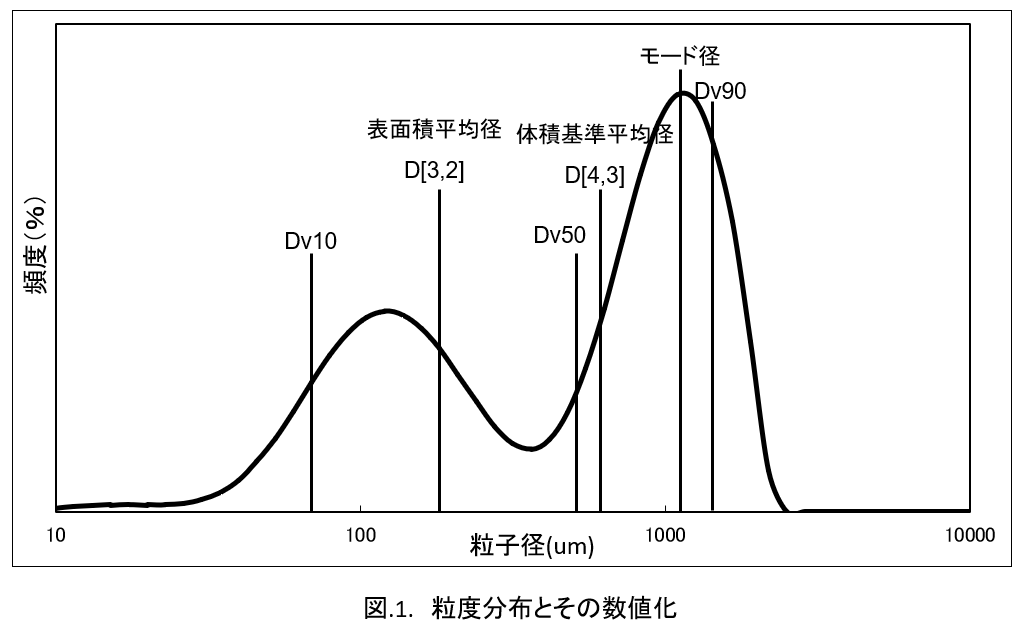
その応用として、粒度分布の取り扱いに特化して用いられる分布として、ロジン-ラムラー分布などがある。
いずれの場合でも、それぞれの目的に応じて数値は使い分けられるべきであり、その数値の意味はよく理解されておくべき事項である。そのいくつかの意味と応用事例などを表 2にまとめた。
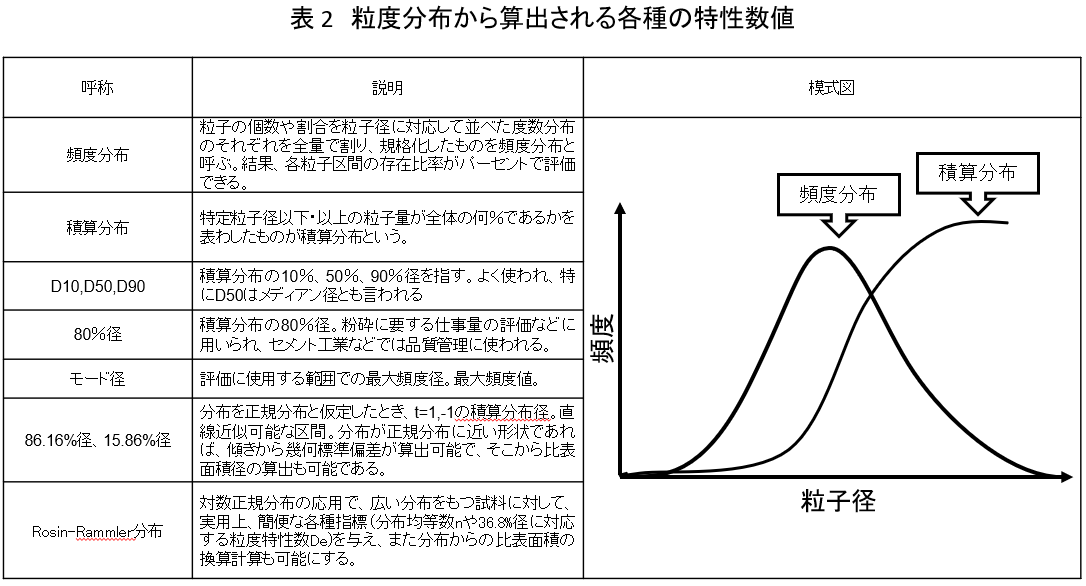
また、粒度分布から得られる各種代表径以外の径として、各種の平均径がある。
これは、定義された指標における全粒子径を母集団(個数・体積など)で除することで得られる。
比較的計算が平易で、簡単に代表値を得やすい方法なので多用される。
粒度分布と平均径を併用して取り扱う上で、最も注意すべきことは、「平均径は、粒度分布を必ずしも表現し得ない」という点である。
例を挙げて説明する。ある手法で計測された粒度分布データが図.2. (a),(b)に示したようにあるとする。
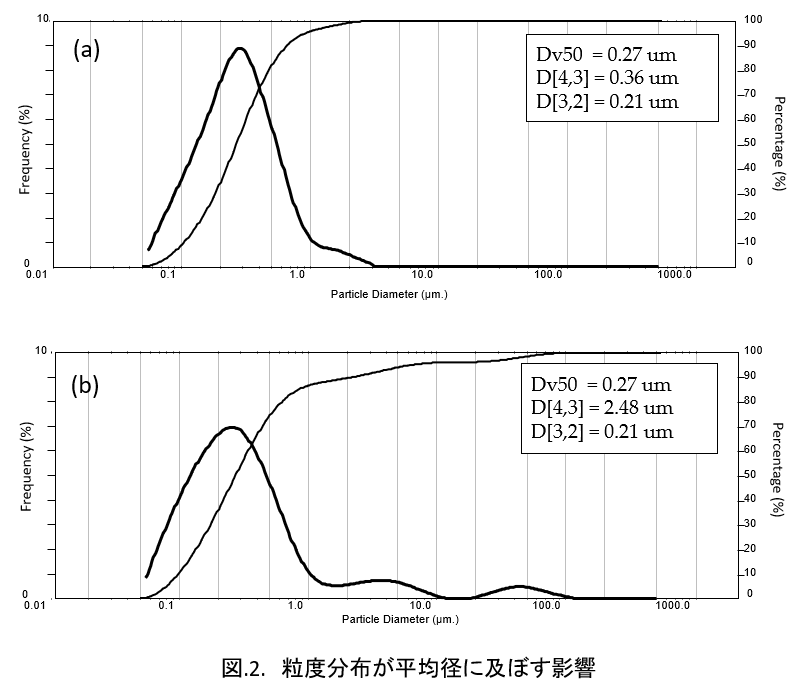
このデータからは、同時に、体積平均径(D[4,3])と表面積平均径(D[3,2])も計算可能である。この事例では、(a)、(b)においては、Dv50 =0.27μm、D[3,2]=0.21μmと同じ大きさとして算出されている。
しかし、D[4,3]は、粗大粒子の影響で(a)が0.36μmであるのに対して、(b)が2.48μmと大きく算出されている。
ここから明らかなのは、母集団の一部で粗大が現れる、微粉が少し増える、などという分布の違いが試料において生じても、粒度分布全体の均衡が確保されるのであれば、分布の代表径(たとえばDv50)は応答しない場合があり、逆に、平均径は母集団の大きさが変化することで数値が応答する可能性がある点である。
したがって、平均径の数値は母集団に大きな影響を受けることを意味し、その適用には注意が必要である。
上記述べてきたように、粒子径は分布をもち、特性数値化も複雑である。
同時に、その適切な測定手法を選択することが重要な項目であるといえる。分布の測定方法には多くの種類がある。
その種類と簡単な原理および分類を表 3 図.3.にまとめた。
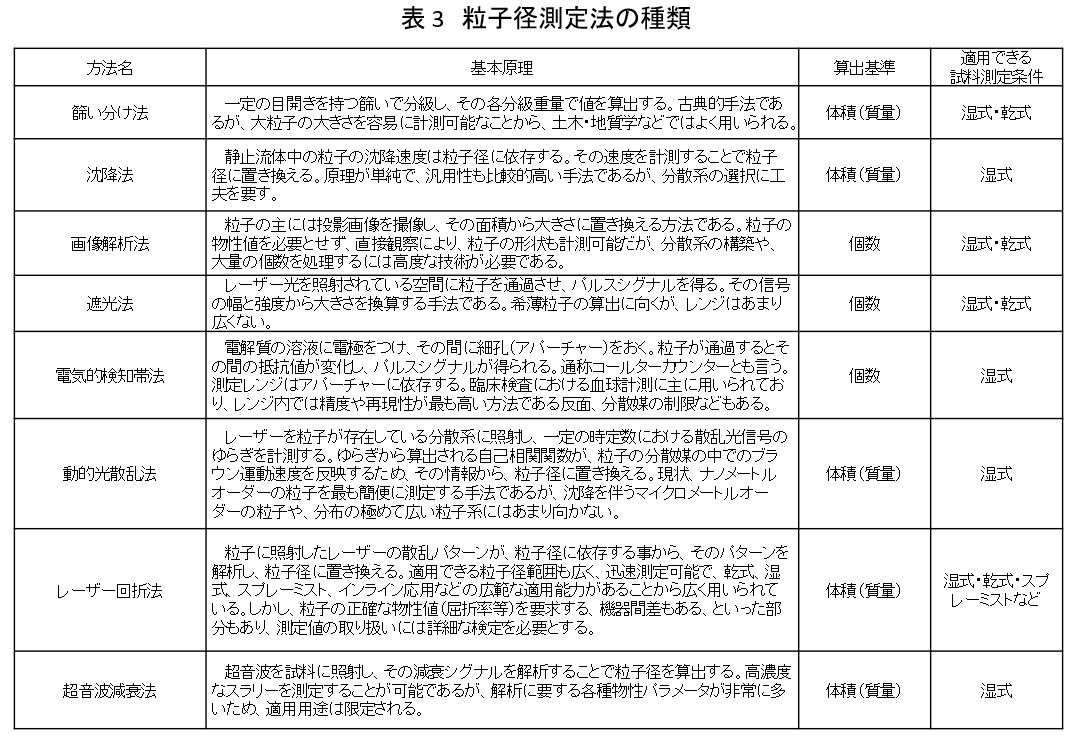
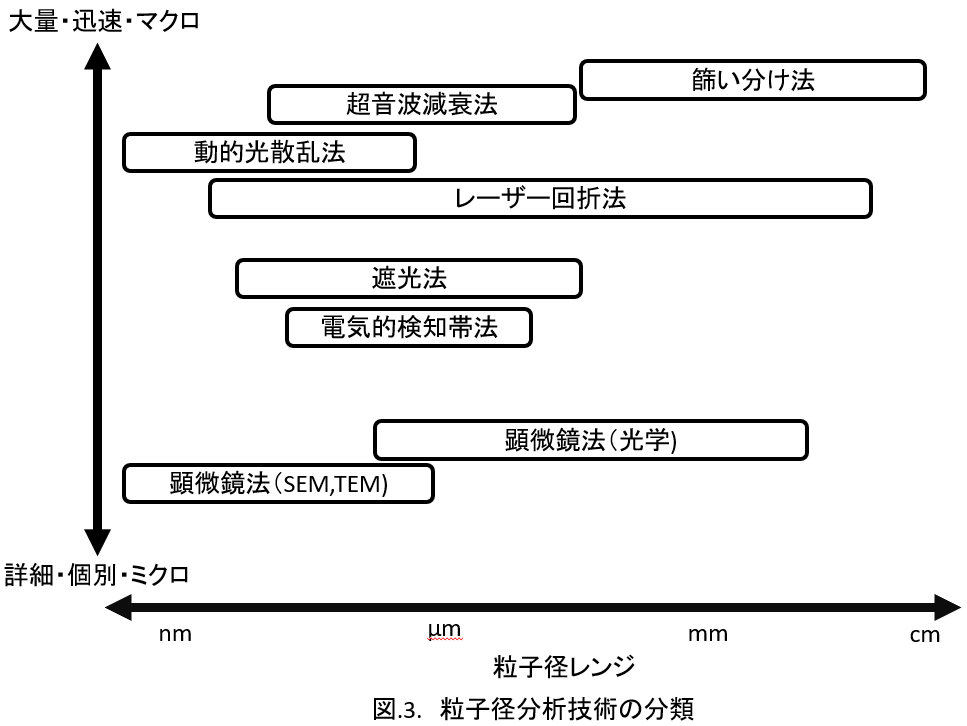
それぞれの詳細は教科書4)などを参照にされたいが、それぞれに得られる基準データが体積・個数とそれぞれに異なるため、原理をよく理解し、適切に使い分ける必要がある。
これまで述べてきたように、粒子径は粒子の基礎的な物性値であり、非常に重要である。
しかし、一方で、統計的取り扱いをするために、形状(Particle Shape)を仮説的に近似、あるいは一部、無視せざるを得ない。
しかし、粒子を評価するにあたっては、その形状が与える種々の特性評価も重要な要素であり、考慮すべき事項である。
粒子径の評価に関し、米国薬局方(USP) 776 においては、"...For irregularly shaped particles、 characterization of particle size must include information on particle shape.
(…不規則な形状の粒子について、粒子径の特性は、形状の情報を含めなくてはならない) "と記載されている。
これは、粒子を評価するときに、その粒子の形状が粒度分布に及ぼす影響が少なくないことを意味する。
また、Heywoodもマーティン径とフェレー径に対し、それぞれの算出値に形状の影響が存在することを述べている6)。
その具体的事例を図.4.に示した。
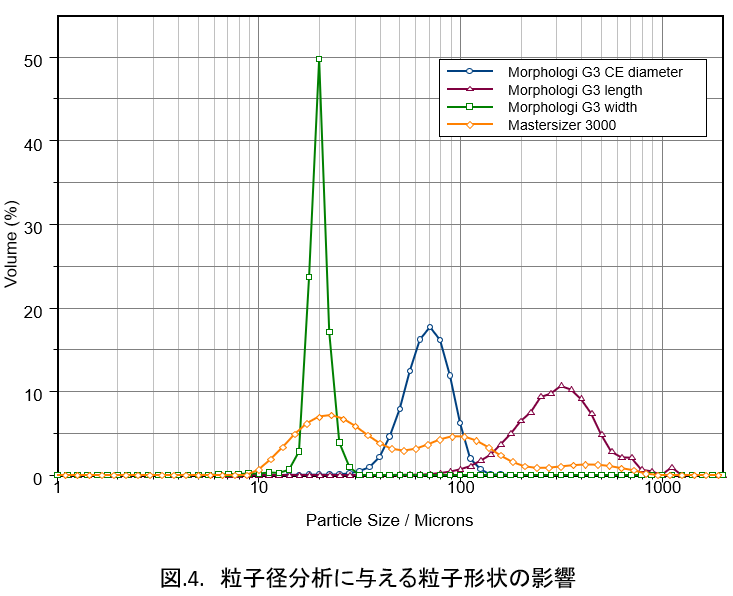
試料は、長さ、幅の揃った柱状グラスファイバー試料をMalvern社製レーザー回折式粒度分布装置マスターサイザー3000で測定した事例である。
このデータからは3つの分布成分があるように見えるが、現実は単一粒子で構成されており、現実とは乖離する。
これを粒子画像解析装置 Malvern社製MorphologiG3を用いて検討すると、それぞれの分布は、長軸径、円相当径、短軸径にそれぞれ相当することが明らかになった。
これは、レーザーの照射方向に依存して散乱パターンが異なることに起因するものであり、形状に算出粒子径が依存するという事例である。
粒子形状値は主には任意の大きさの次元を持つ径(スカラー量)同士の比で示される。
その数値化するアルゴリズム例を図.5.に示した。これらの数値がどのように算出されているか、そして、どのような意味をもつかを理解することは重要である。
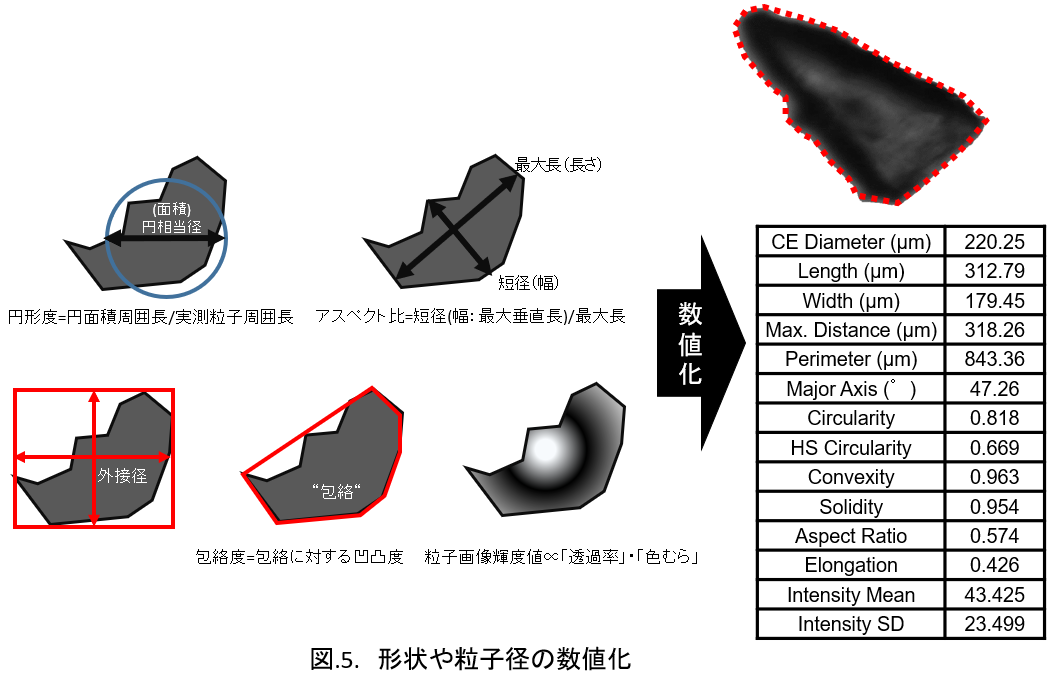
従来、粒子形態、特に粒子の形状の数値化は顕微鏡観察に基づく手作業が主に用いられてきた。
このため、人による誤差や解釈の違いが生まれると同時に、大量の粒子に関する情報を取り込むことが困難であった。近年、コンピューターの進歩とともに、撮像した多数の粒子画像データを高速に取り扱うことが可能となったことから、統計的に有為な情報として取り扱うことが可能となったことから、粒子形状の高度数値化に、近年よく用いられるようになりはじめた手法である。
[A4] 本法は、ISO13322-1,2に”Image Analysis Method”として記載されている手法を基本としている。粒子を1 粒子ごとに画像解析することで、粒子径のみならず、形状も同時に評価可能な手法である。
粒子を固定して撮像系を動作する、静的画像分析法(Static Image Analysis)と撮像系を固定し、粒子を分散系に分散するなどして高速で移動して画像を取得する動的画像分析法(Dynamic Image Analysis)の2種類がある。
いずれの手法も、解析プロセスは大きくは変わらない。撮像した粒子画像をCCDやCMOSのピクセルで周囲(バックグラウンド)と分画し、2値化して粒子のみを切り出す。
その後、そのピクセルをカウントして径(円相当径など)に換算する。
また、その画像の形状から円形度、包絡度、アスペクト比なども同時に計算可能である。
得られる結果は、個数基準、体積基準粒子径と形状である。画像イメージング法では、粒子一つ一つを撮像するため、異形粒子の判別がしやすい。
特に、同じ粒度分布でも、形状が異なると、粒度分布などに影響を与える可能性もあるため、その数値化された粒子の評価は肝要である。
また、一次粒子であったとしても、凝集すれば粒子の形状が歪に観察される。これを利用することで、粒子の凝集などの判別に基づく凝集率の算出も可能である。
さらに最近、単純な形状だけではないもう一つの指標として、粒子の透過率や反射率といった観察した様相を数値化することも可能になってきた。
これは、粒子の画像を取得したカメラの画像データが構成している各ピクセルの光線に対する輝度値をデジタル的に、たとえばグレースケールの256階調などを用いて数値化する。
1粒子を構成する画像には、多数のピクセルがあるので、その1画像の平均値や偏差を計算することで、粒子の「見た目」を数値化できる。
この技術により、各粒子の密度や厚みにかかわる特性を定性的ではあるが、数値を伴って分類可能であるので、形状以外の粒子分類法として有用なパラメータである。
ここまで、粒子径分析に関する定義や測定法にかかわる事項について解説してきたが、結局のところ、「どの粒子分析が最適であるか?」という点についてはこれまでの説明では、明確な回答は困難である。
そこで、一つのアプローチとして、粒子分析法を、試料測定に適用できる部分にのみ着目して分類して、ランク付けしたものを表 4に示した。
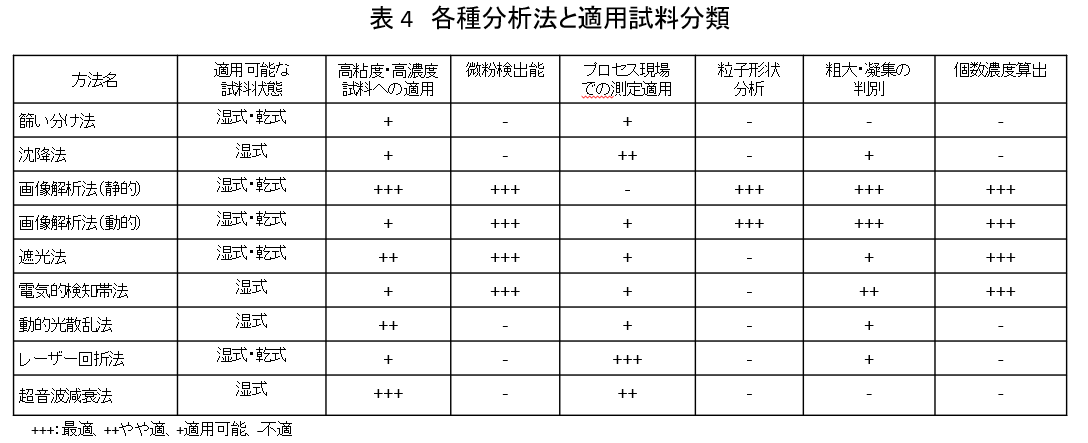
ここからも、すべての試料に対し適用できる分析法を作ることは困難であり、試料や目的に応じて使い分けされなくてはならないが、その最終目的に応じて使い分けることで、目的合理性のある分析法が構築できることが示唆された。
本論で述べてきた内容は、筆者が粉体や粒子について、各種の技術セミナーや大学・研究機関・一般企業のなどで講演させていただく機会を得た際にお話させていただいた内容と、
ご参加いただいた方から頂いたご質問や、その時にご回答した内容などを多く含んでいる。
したがって、基本的な原理を詳細に述べるよりも、現実に直面する課題に対して、少しでもヒントになればという視点を主な目的として執筆した。
粒子分析に限らず、分析技術とは目的を達成する手段であり、目的は研究そのものの抱える課題の解決や製造工程などでの潜在的なリスクを減らすことなどである。
しかしながら、分析化学一般において、分析結果・技術がいわば独り歩きし、しばしば手段が目的にすり替わってしまうことがある。
特に粒子分析は、Heywood先生のお言葉にもあったように、目的合理性を求められる分析法であり、「最適な」適用法がいまだに模索されている。
本稿が、その最適な運用法の構築に少しでもお役に立てれば幸いである。
参考文献
1) Shinkuma D., et.al., Yakuzaigaku, 39, 121-128 (1979).
2)三輪茂雄. 粉体工学通論. 日刊工業新聞社 (1981)
3) Green,H.,J.Franklin Inst.,204, 713-729 (1929)
4) Galton, F., : Proc. Roy. Soc., 29, 365-367(1879)
5) 粉体工学会 編. 粒子径計測技術 .粒子径計測技術(1994)
6)Heywood,H., Chem.& Ind., 56, 149-154(1937)