제타 전위는 현탁액에 들어있는 입자에서 나타나는 물리적 특성입니다. 현탁액, 에멀젼 그리고 단백질 용액들의 표면에서의 상호작용을 예측하여 필름 조성이나 코닝액의 조성을 최적화 하는데 이용할 수 있습니다. 제타 전위에 대한 이해를 통해 제품 개발 시간을 단축시킬 수 있습니다. 또한 장기 안성성을 예측하기 위하여 사용되고 있습니다.
거대분자의 전하, 또는 보다 구체적으로 단백질의 전하, 측정을 위하야 새로운 제타사이저 ZSP 같이 매우 민감한 시스템이 필요하며, 샘플량을 감소시킬 기술과 시료의 분해를 방지할 수 있는 기술이 필요합니다. 시스템과 기술에 대한 자세하 내용은 MRK 1846에 설명되어 있습니다.
제타사이저 나노시리즈를 이용하여 표면 제타전위 측정하기 위해서는 악세사리가 필요하며 그 주요 특징은 MRK 1749에 설명되어 있습니다.
이러한 도입은 그들이 분산 된 상태의 경우, 침전이 무시할만큼 그러한 낮은 밀도, 콜로이드 시스템의 제타 전위에 집중한다.
물질에는 고체, 액체, 기체 3가지의 기본 상이 있습니다. 3가지 상중에 하나의 상이 매우 잘 분산되어 있는 상태를 '콜로이드 시스템'이라고 합니다. 이러한 물질들은 실용화를 위해 중요한 속성이 있습니다.
콜로이드 시스템에는 에어로졸, 에멀젼, 콜로이달 현탁액 그리고 결합성 콜로이드 등의 여러 종류가 있습니다.
특정 상황에서, 분산액 중의 입자가 서로 밀착 중력의 영향 하에서 정착있다 순차 증가하는 크기의 응집체를 형성 할 수 있습니다. 초기에 형성된 응집체들을 floc이라고 부르며 이러한 과정을 응집이라고 합니다, 이러한 플럭들은 침전 또는 상분리가 일어나거나 그렇지 않을 수 있습니다. 응집체들이 더 단단해지면 응고라고 불립니다. 일반적으로 응집체들은 침전되면서 상분리가 일어나거나(분산매보다 무거운 경우) 크리밍 현상이 일어납니다(분산매보다 가벼운 경우). 응집과 응고는 종종 동일한 용어로 사용되고 있습니다. 일반적으로 응집은 가역적으로 해교될 수 있으나 응고는 비가역적입니다. Figure 1에 대표적인 응집 과정에 대하여 나태내습니다.
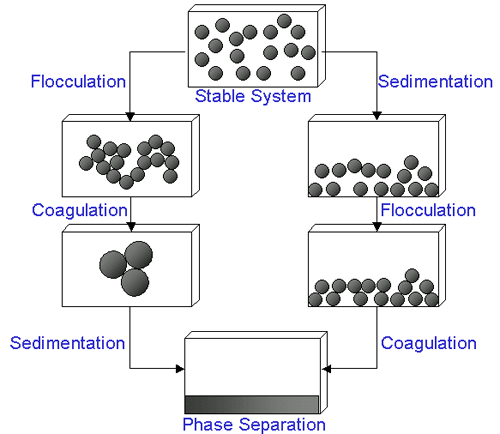
|
DLVO 이론은 Derjaguin, Verwey, Landau 그리고 Overbeek의 과학자에 의해 1940년에 개발된 이론으로 콜로이드 시스템의 안정정을 다루고 있습니다. DLVO이론은 용액 내 입자의 안정성은 총 포텐셜 에너지 함수 VT에 의존하는 것으로 제안하였습니다. VT 는 아래의 몇몇 기여도에 따라 결정됩다.
VT = VA + VR + VS
VS 는 용매에 기인하는 포텐셜에너지이고, 총포텐셜에너지의 마지막 몇몇 나노입자들의 분리에 관여되는 기여도가 가장 작은 텀입니다. 더 중요한 인자는 VA 와 VR 사의의 균형으로, 이는 인력과 척력의 분포를 나타냅니다. 포텐셜적으로 좀 더 크고 큰 거리에영향을 미치는 VA 는
VA = -A/(12 π D2)
여기서 A는 Hamaker상수이고 D는 입자 분리도 입니다.
척력을 나타내는 포텐셜인 VR 은 좀 더 복잡한 식으로 표현됩니다.
VR = 2 π ε a ζ2 exp(-κD)
a 는 입자 반경, π 는 용매의 용해도이고 κ 는 이온조성, ζ 는 제타전위를 나타내는 함수입니다.
DVLO 이론은 colloidal 시스템에서의 안정성은 입자간에 브라운 운동시에 존재하는 반데르발스의 인력과 전기이중층에 의한 척력의 합으로 결정됩니다. 분리되려고 하는 힘, 즉 반발력을 점선으로 뭉치려고 하는 힘(반데르발스의 힘) 실선으로 Figure 2a에 나타내었습니다. 이론은 두 입자가 접근하는 것을 막는 척력과 두 입자가 결합하려는 것에 기인하는에너지장벽을 나타내고 있습니다. 하지만 이러한 에너지 장벽을 넘지 못한 입자는 인력이 작용하여 비가역적으로 서로 뭉치게 됩니다.
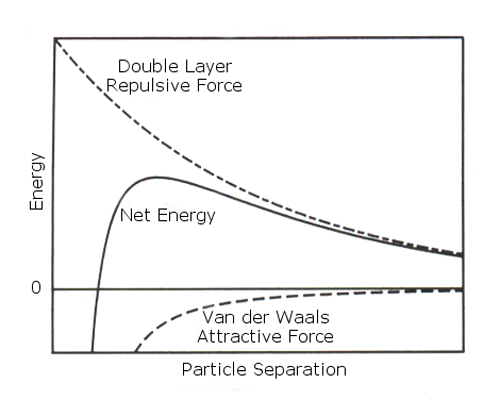
|
따라서, 만약에 입자가 충분히 높은 반발력을 가지면dispersion 은 응집이 일어나지 않게되고 colloidal 시스템은 안정하게 될 것입니다. 그러나 반발 메카니즘이 존재하지 않는다면 응집이나 응고가 일어나서 결국에는 침전이 일어날 것입니다
만약에 제타전위가 감소하면(고농도의 염인경우) 입자 사이에 더 약하고 포텐셜적으로 가역적인 결합이 있을 경우 "2 차 최저점"이 생성될 가능성이 있다.(figure 2 (b)) 이러한 약한 floc 은 브라운 운동에 의해 깨지지 않을만큼 안정하지만, 강제적인 교반등에 의한 외부적인 힘이 작용하면 분산이 일어난다.
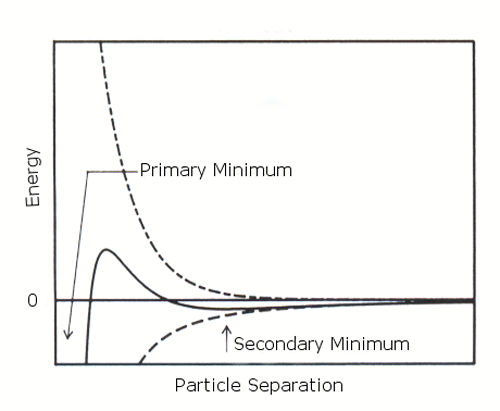
|
그러므로 colloidal 시스템의 안정성을 유지하는 것은 반발력이 지배적으로작용해야 한다. colloidal 시스템의안정성은 어떻게 이룰 수 있는가? dispersion 의 안정성에 영향을 미치는 두 개의 근본적인 메카니즘이 있다.(figure 3):
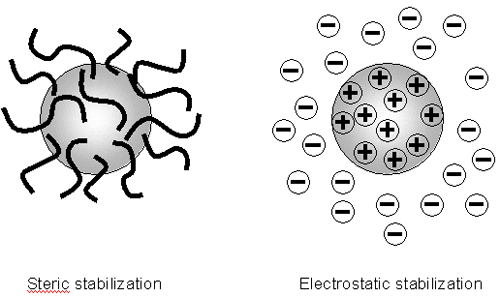
|
각각의 메카니즘은 개개의 시스템에 유리한 점이 있습니다. 입체 안정성은 간단하고 적합한 고분자만 있으면 가능합니다. 하지만 고분자는 가격이 비싸질 수 있고 예를 들어 세라믹 슬립은 캐스팅과 소결시에 고분자는 타버려서 메카니즘에 맞지 않는 경우가 있습니다. 또한 이것은 수축을 일으키며 결점으로 작용 합니다.
정전기적 혹은 전하안정성은 단순한 시스템내의 이온의 밀도를 바꾸는 안정화나 응집시스템에 장점이 있습니다 이것은 가역적 프로세스이고 비싸지 않다.
제타전위는 오랫동안 콜로이드 입자간의 상호작용 정도를 측정하는 좋은 지표로 알려졌고, 제타전위의 측정은 일반적으로 콜로이드 시스템의 안정성 확인에 사용해왔습다.
수용성 매체에 있는 대부분의 콜로이드 분산은 전하를 옮깁니다. 입자의 기본 성질과 그 주위환경에 의존하는 표면전하에 대한 많은 원인이 있지만 우리는 더 중요한 메카니즘에 대해 고려할 것입니다.
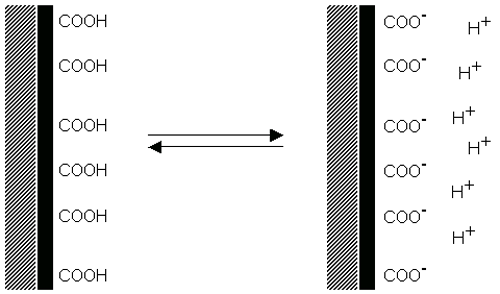
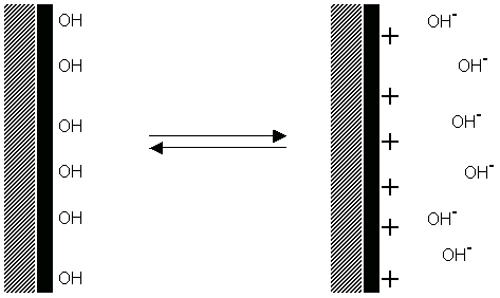
입자 표면의 acid 그룹의 분해는 표면에 음전하를 띄게 하고 반대의 과정은 입자표면에 base 그룹의 분해에 의해 염기 양전하를 띄게 합니다(figure 4). 두 가지 경우에 표면의 전하량은 산성과 염기의 강도와 표면 그룹에 있는 용매의 pH 에 의존합니다. 표면의 전하는 음전하입자 표면의pH 의 감소로 인한 이온화 억제(Figure 4(a)) 혹은 양전하의 pH 증가로 인해 0 으로 감소할 수 있습니다(Figure 4(b)).
|
|
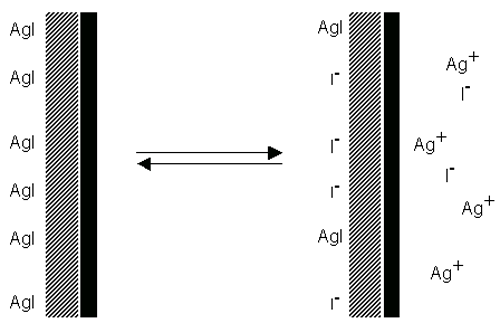
예를 들어, 물속에 있는 요오드화은을 생각해보자. 결정격자로 부터의 이온의 차등손실 만약 같은 양의 Ag+와 I-가 용해되어 있다면 표면은 전하를 띄지 않을 것입니다. 사실 은이온은 우선적으로 용해하면서 표면에 음전하를 띠게 됩니다.(figure 5). 만약 Ag+ 이온이 첨가된다면 전하가 0 으로 떨어질 것이고 더 첨가하게 되면 표면은 양전하를 띠게 될 것입니다.
|
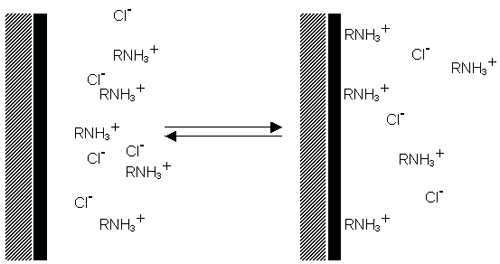
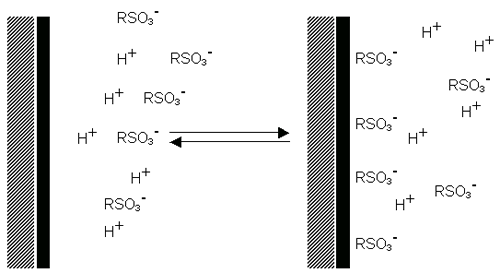
계면활성제 이온은 양이온 계면할성제의 경우 명확하게 입자의 표면에 흡착되어 양전하 표면을 가지게 되고(Figure 6(a)), 음이온 계면활성제의 경우는 음전하 표면을 가지게 됩니다(Figure 6(b)).
|
|
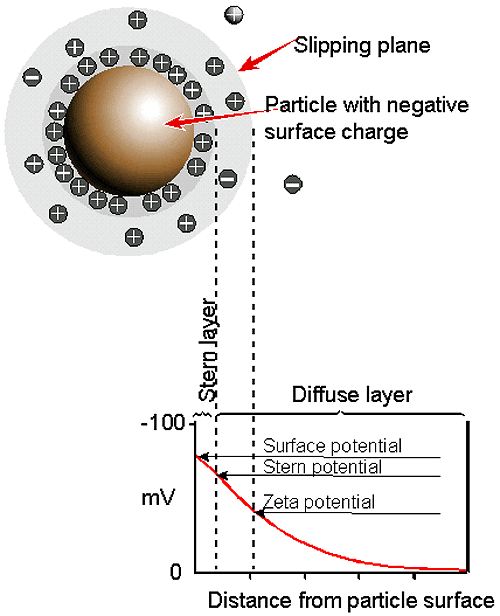
입자표면에서의 최종 전하의 결정은 카운터 이온(표면에 근접한 입자의 반대의 전하를 가지는) 이온의 밀도 증가로 인한 주위 접촉영역 이온의 분포에 영향을 미치게 됩니다. 이와 같이 전기적이중층은 각각의 입자주위에 분포하게 됩니다.
입자 주위에 존재하는 액상층은 두 가지가 있습니다; 이온이 강한 경계를 이루고 있는 내부영역(Stern layer:전자층)과 보다 약하게 결합되어있는 외부영역(defuse)으로 구성되어 있습니다. 외부영역은 이온과 입자가 안정하게 존재하는 이론적인 경계입니다. 예를 들어 입자가 움직이면(중력에 영향을 받는 경우) 이온은 경계 내에서 움직입니다. 경계의 밖에 있는 이온은 거대한 분산제와 같이 존재합다. 이 경계의 포텐셜(표면의 유체역학 적인 전단응력)이 제타전위입니다. (figure 7).
|
이러한 제타전위의 크기는 콜로이드 시스템의 포텐셜적인 안정성을 나타냅니다. 서스펜젼에 있는 모든 입자가 큰 음전하 혹은 양전하의 제타전위를 가지고 있을 때 서로 많이 반발하는 경향을 가지게 되고 이들은 서로 결합하려 하지 않습니다. 그러나 낮은 제타전위를 가지게 되면 입자들이 서로 반발하는 힘이 없을 것이고 결국 응집이 일어나게 됩니다.
일반적으로 안정하거나 불안정한 서스펜젼을 나누는 기준은 +30 또는 -30 밀리볼트의 입니다. 입자의 제타전위 값이 절대값으로 30mV이상을 갖는 경우 일반적이로 안정하다고 말할 수 있습니다. 그러나 입자가 분산제와 다른 높은 밀도를 가지게 될 경우 침전이 일어나 팩베드 형상(밀가루 반죽)을 띄게 됩니다.
따라서 제타전위는 분산제의 특성 뿐만 아니라 표면에 영향을 받으며, 상이한 물질의 제타 전위를 비교하는 경우 입자의 제타전위는 분산제의 성질 또한 포함하고 있음을 알 수 있습니다.
제타 전위 측정에 영향을 주는 변수는 아래와 같습니다.
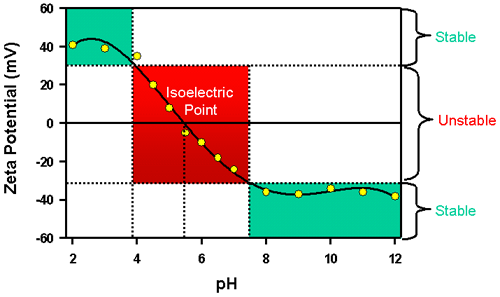
수용액에서는 샘플의 pH 가 제타전위에 가장 중요한 인자로 작용합니다. 서스펜젼내의 음전하를 띄는 입자가 있다고 가정해보겠습니다. 알칼리를 서스펜젼에 첨가를 하게 되면 입자들은 점점 더 강한 음전하를 띄게 됩니다. 서스펜젼에 산을 첨가하면 전하는 중성을 띄는 점까지 도달하고 될 것입니다. 산을 계속적으로 첨가하면 양전하를 띄게 될 것입니다. 이 경우, pH에 따른 제타전위 곡선은 낮은 pH에서는 양의 값을 높은 pH에서는 음의 값을 나타내는 갖게 될 것입니다. 그리고 pH에 따른 제타전위를 나타낼 때 전위값이 0이 되는 경우를 등전점이라고 하며 입자를 이햐할 수 있는 중요한 값입니다. 일반적으로 콜로이드 시스템에서 등전점보다 높아야 최소한의 안정성을 유지할 수 있습니다
pH에 따른 제타전위의 전형적인 변화를 Fig 8에서 확인 할 수 있습니다. 이 예에서 알 수 있듯이 시료의 등전점이 대략 pH5.5임을 확인 할 수 있습니다. 그리고 pH 4이하일 경우(양전하가 충분히 존재한다면)와 pH 7.5보다 클때(음전하가 충분히 존재한다면)의 안정성을 예측 할 수 있습니다. pH4~7.5에서의 제타전위가 +30에서 -30mV 사이 값을 가질때 분산 안정성에 대한 분제가 생길 수 있습니다.
|
이중층의 두께(κ-1)는 용액 내 이온의 농도에 따라 결정되고 이는 용액내의 이온의 힘에 따라 계산 할 수 있습니다. 이온의 힘이 크다면 더 압축된 이중층을 형성 할 수 있습니다. 이온 또한 이중충의 두께에 영향을 미칩니다. Al3+와 같이 알루미늄 3 가의 이온은 Na+같이 1 가의 이온을 가지는 것과 비교했을 때 더욱 두꺼운 이중층을 형성합니다.
무기물이온은 둘 중 하나의 방법으로 표면의 전하에 영향을 받을 수 있습니다. i)등전위점에 영향을 미치지 않는 이온흡착이 나타나지 않는 경우 ii)등전위점에 영향을 미칠 수 있는 특정이온에 흡착이 일어나는 경우 입자표면에서의 이온 특정흡착은(비록 낮은 농도일 경우에도) 입자분산의 제타전위에 거대한 영향을 미칩니다. 몇몇의 경우에는 특정 이온흡착으로 전하가 역전되는 경우도 발생합니다.
제타전위의 구성요소에 대한 농도의 영향은 최대한의 안정성을 가질 수 있는 정보를 알려줍니다. 시료의 제타전위에 대해 알려진 물질의 영향은 침전을 막는 좋은 도구가 된다
입자표면에 존재하는 전하가 중요한 것은 인가된 전기장과 상호반응 하기 때문입니다. 이러한 효과를 전기역학적 효과라고 정의한다. 4가지의 효과에 따라 움직임이 유도 됩니다. 요소들은 다음과 같습니다.
전기 영동: 인가된 전기장에 영향을 받는 서스펜션에서의 입자의 움직임
전기 삼투: 인가된 전기장에 영향을 받아 고정된 전하 표면에서 용액의 움직임
전위 흐름: 고정된 전하 표면으로 빠른 흐림이 생길때 발생하는 전기장
전위 침전: 전하를 띈 입자가 침전될때 발생하는 전기장
전해질에 전기장이 제공될 때 전하를 띤 입자가 전해질에 들어가면 반대의 전하를 가지는 전극에 유인됩니다. 점성력은 이 움직임에 반대되는 경향이 있습니다. 이 두 힘이 중성에 도달하면 입자는 일정한 속도를 가지게 됩니다.
이 속도는 전기장의 힘이나 전압의 변화, 용매의 유전 상수, 용매의 점도, 제타전위에 영향을 받습니다.
단위전기장에서의 입자의 속도는 전기흐름의 이동성과 관련이 있습니다. 제타전위는 Henry equation 으로 정의되는 전기흐름의 이동성과 관련이 있습니다.
UE = 2 ε z f(κa) 3η
UE 는 전기흐름의 이동성이고 z 는 제타전위, ε 는 유전상수, η 은 점도이고 f(κa)는 헨리상수 입니다.
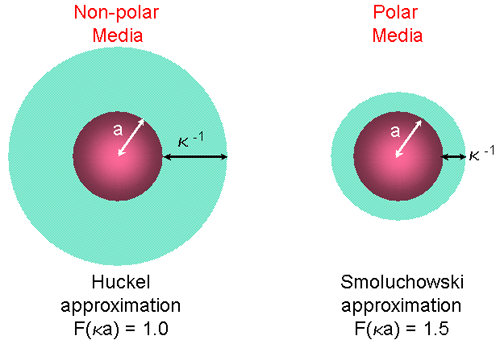
드바이(전기이중극모멘트의단위)의 길이로 정의되는 κ 의 단위는 상호길이를 나타내고 κ-1 은 종종 전기적 이중층의 “두께”로 사용됩니다. a 는 입자반경을 나타내고 따라서κa 는 전기적 이중층의 두께에 대한 입자반경의 비로 나타낼 수 있습니다(figure 9). 제타전위의 전기영동의 결정은 대부분 수용액 상태에서 진행되거나 알맞은 전해질 농도에서 결정됩니다. 이러한 경우에 F(κa)는 1.5 이고 이는 Smoluchowski 의 가정으로 알려져 있습니다. 그러므로 유동성에 근거한 제타전위의 계산은 즉, 10-3 몰의 소금이 있는 전해질에 분산되어있는 0.2 마이크론보다 큰 입자를 다루는 Smoluchowski 모델에서 정확하게 맞는다.
|
낮은 유전률의 용매에 있는 작은 입자의 경우 F(κa)값은 1 이고 간단한 계산이 가능합니다. 이것은 Huckel 가정으로 알려져 있습니다.
마이크로 전자이동 시스템의 요소는 전위차가 존재하는 전극이 있는 모세관 셀 입니다. 입자가 전극으로 이동하면 그들의 속도가 측정되고 이것이 입자의 유동성에 대한 단위필드 힘으로 나타난다.
기존의 방법들은 울트라 마이크로스코프를 이용해서 직접적으로 개개의 입자들을 관찰하고 측정된 거리로서 계산하여 제타 전위를 얻을 수 있습니다. 이것은 아직 세계적으로 많이 사용하는 방법임에도 불구하고 몇몇 불편함이 있으며 특히 작거나 산란이 불안할 때 측정하기까지 매우 많은 노력이 필요합니다. 말번사의 Zetasizer Nano 분야의 기술은 M3-PALS 이장착된 레이저 도플러 전자 이동 방식입니다.
제타사이저 나노 시리즈는 입자의 전기영동을 측정할 수 있는 M3- PALS(특허)의 레이저 도플러점도측정기와 상분석 광산란장치의 조합을 사용하고 있습니다. M3-PALS 방법은 매우 낮은 유동성을 갖는 샘플의 제타전위도 측정이 가능하며 유동성 분포 또한 계산할 수 있습니다.
PALS 는 기존의 측정방법보다 100 배나 효율적입니다. 이것은 높은 전기전도도 물질의 측정도 가능하고 비전해질에 분산되어있는 유동성이 낮은 물질의 측정도 정확하게 할 수 있습니다. 낮은 전압을 사용함으로서 줄발열을 통한 시료에 주는 영향을 최소화할 수 있습니다.
레이저 도플러 전기영동 기술과 M3-PALS 에 관련된 많은 논의와 다양한 논문을 Malvern Instruments 웹사이트에서 찾을 수 있습니다.
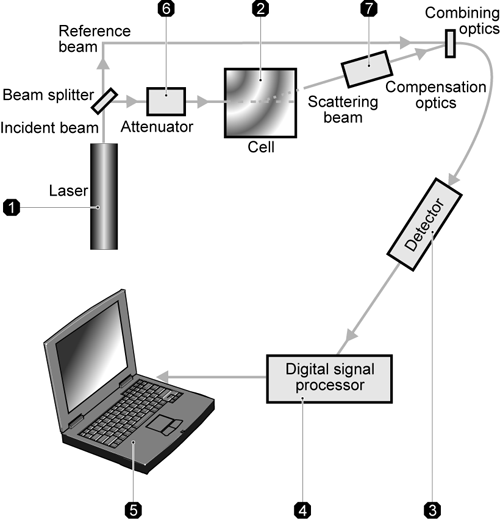
제타전위 측정 시스템은 여섯개의 요소로 결합되어 있습니다(figrue 10) 첫번째로 샘플의 입자를 감지하는 소스로서 레이저를 사용합니다. 제타전위측정을 위하여 레이저는 시료통과를 위한 입사광과 레퍼런스빔으로 나누어 집니다. 입사광은 시료셀의 중앙을 통과하여 13도에서 산란된 빛을 감지합니다. 전기장이 측정셀에 공급되면 측정범위 내에서 움직이는 모든 입자들은 빛의 산란을 야기하게 되고 입자의 속도가 주파수에 비례하는 변화를 감지하며 이러한 정보들은 전자식 신호프로세서로 입력되고 컴퓨터로 전송됩니다. Zetasizer Nano software 는 전자이동 유동성의 주파수 스펙트럼을 만들고 제타전위를 계산합니다. 검출기에 산란된 빛의 강도는 특정한 검출 범위 내에서 성공적으로 측정됩니다. 조절된 빛은 샘플에 도달하게 되고 산란의 강도가 생기는데 이것은 6 번의 감쇠기에서 감지하게 됩니다. 측정셀의 두께 차이와 분산매의 굴절률의 상이한 점에 대한 정확한 측정을 위해 보상광학체인 7 번을 설치하고 최적의 조건을 유지한다
|
Derjaguin, B.V. and Landau, L. (1941) Acta Physiochim. URSS, 14, 633.
Verway, E.J.W. and Overbeek, J. Th. G. (1948) Theory of the Stability of Lyophobic Colloids, Elsevier, Amsterdam.
Hunter, R.J. (1988) Zeta Potential In Colloid Science: Principles And Applications, Academic Press, UK.
Shaw, D.J. (1992) Introduction To Colloid And Surface Chemistry, Butterworth Heinemann, UK.
Everett, D.H. (1994) Basic Principles Of Colloid Science, The Royal Society of Chemistry, UK.
Ross, S. and Morrison, I.D. (1988) Colloidal Systems and Interfaces, John Wiley and Sons, USA.
Lyklema, J. (2000) Fundamentals of Interface and Colloid Science: Volume 1 (Fundamentals), Academic Press, UK.
Measuring Zeta Potential: Laser Doppler Electrophoresis, Technical Note available from www.malvern.com
Measuring Zeta Potential Using Phase Analysis Light Scattering (PALS), Technical Note available from www.malvern.com
Measuring Zeta Potential: A New Technique, Technical Note available from www.malvern.com
Simplifying the Measurement of Zeta Potential Using M3-PALS, Technical Note available from www.malvern.com