레이저 입도분석기의 이해와 입도분석 원리

입도분석의 기본 원리

 

 

입자란 ?

이것을 묻는 것은 아주 어리석은 질문이다. 하지만 다양한 입자 크기 분석 기술에 있어서 이러한 것은 기초가 된다. 분산 과정과 재료의 모양은 입자 크기 분석에 있어 처음보다 더욱 복잡해진다.

 

 

입자 크기 문제

 

성냥갑을 주고 누군가가 이 성냥갑의 사이즈가 얼마인지 말해보라고 물었다고 가정해보자.  

아마도 이 성냥갑의 크기가 20*10*5mm 라고 대답할 것이다.  

“성냥갑의 크기가 20mm”라고 정확하게 대답할 수 없을 것이고, 이러한 것은 크기를 말하는데 하나의 견해일 것이다. 그래서 당신은 한 개의 고유 치수로는 3 차원으로 된 성냥갑을 묘사 할 수 없다.   

 

명백하게 이러한 상황은 모래의 입자나 페인트 깡통 안의 색소입자와 같은 복잡한 모양에서는 더욱 어려워진다.  

 

내가 만약 Q.A.(품질관리) 매니저라면, 입자를 묘사하는데 하나의 숫자가 원할 것이다 – 예를 들어 마지막으로 만들어진 제품의 평균 크기가 증가되었는지 감소되었는지 알기를 원할 것이다. 이것은 입자 크기 분석문제에 기본적인 문제이다. – 어떻게 우리는 오직 하나의 숫자로 3 차원적인 물체를 표현할까? 

 

 


Figure 1 은 몇몇 모래의 입자를 나타내었다. 그것들의 사이즈는 무엇인가? 

 

 

상당구(Equivalent spheres) 

 

 하나의 유일한 숫자로 표현 가능한 구가 있다. 만약 우리가 50μm 크기인 하나의 구를 말할 때 이것은 정확하게 표현 가능하다. 50μm 크기 큐브의 모서리와 대각선을 말할 때는 표현을 할 수 없다.  

 

많은 특징이 있는 성냥갑은 하나의 숫자로 표현 가능하다. 예를 들면 부피와 표면적에 관련한 무게는 하나의 특정한 수이다. 그렇다면 만약 성냥갑의 무게를 측정하는 기술이 있다면 우리는 성냥갑의 무게를 구의 무게로 변환할 수 있다.  

 

기억해야 할 것은  

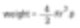
그리고 성냥갑과 같은 무게의 구의 직경에 대한 하나의 특정수(2r)를 계산한다. 이것이 equivalent sphere 이론이다.  

 

우리는 어떤 입자의 성질을 측정하고 구라고 언급한 입자를 가정한다. 그러므로 입자를 표현하기 위한 하나의 특정한 수(구의 직경)로 얻는다.  

 

이것은 3 차원입자를 표현할 때 비록 제어 목적을 위해 더 정확한 것은 불편할지 모르지만 3 또는 그 이상의 수로서 표현할 필요가 없다는 것을 말해준다.  

 

 

이것이 물체의 모양에 의존하는 흥미로운 효과들을 알 수 있고 예로써 구와 같은 실린더를 도시하였다. (Fig.2)  

 

그러나 만약 실린더의 모양이나 크기가 변한다면 부피/무게는 달라질 것이다. 그리고 등가 구형 모델로서 우리는 최소한 그것은 더 작아지거나 커졌다고 말할 수 있다. 

 

 

100 x 20μm 실린더의 상당구 (Equivalent spherical) 지름 

 

실린더의 직경이 D1=20μm 높이 100μm 이라고 생각해보자. 직경이 실린더와 부피가 같은 D2 의 직경을 가진 구가 있다. 우리는 다음과 같이 직경을 계산할 수 있다.  

 

실린더의 부피  

 

 

구의 부피  

 

 

X 는 부피 반경 값이다. 

 

 

100μm 높이와 20μm 직경의 실린더의 구형직경의 부피는 대략 40μm 이다. 밑의 표는 다양한 비율의 실린더의 구형의 직경을 나태내고 있다. 마지막 줄은 전형적인 디스크모양의 큰 클레이 입자일 것이다. 그것은 높이 20μm 에 0.2μm 의 두께를 가지기 때문에 일반적으로 차원을 고려하지
않아도 될 것이다.  

 

입자의 부피를 측정하는 도구에 관해 우리는 약 5μm 정도에서 답을 얻을지도 모른다. 따라서 이러한 답에 이의를 제기할 가능성에 대해 다른 기술을 사용해야 한다. 

 


또한 이러한 모든 실린더들은 25μm 인 여과기와 같은 사이즈로 나타날 수 있는데 이때 “모든 물질은 25μm 보다 작다”고 말할 수 있다. 이러한 실린더들은 각각 다른 값을 가지고 있으므로 레이저 회절시 다르게 보여질 수 있다. 

 

 

 

여러가지 측정기술

 

명백하게, 만약 현미경을 통해 입자를 보게 된다면 2 차원으로 투사된 것을 볼 수 있고, 입자를 특징화하여 측정할 수 있는 입자의 직경들이 있다. 만약 우리가 입자의 최대길이를 받아들이고 이것을 우리의 크기로서 사용한다면 우리는 입자가 최대 차원을 가지는 구입자라고 말할 수 있다.  

 

마찬가지로 만약 우리가 최소 직경이나 Feter’s diameter 와 같은 양을 사용한다면 이것은 우리에게 입자의 크기에 관해 또 다른 답을 제공해 줄 것이다. 이 때문에 우리는 각각의 기술은 입자의 다른 물성(최대 길이, 최소 길이, 부피, 표면적 등)을 측정할 수 있다는 것을 반드시 알아야 한다.  따라서 선택적으로 측정한다면 나머지 측정기술과 다른 결과를 보일 것이다.

 

 

 


Fig 3 은 하나의 모래알을 표현 가능하게 하는 다른 몇몇의 해답들을 나타낸다. 각 기술은 잘못되지 않았다 – 기술들은 모두 옳고 입자의 다른 성질을 측정하는 것이다. 그것은 cm 나 inch 법으로 성냥갑을 측정하는 것이다(당신은 길이를 측정하고 나는 폭을 측정한다!). 

 


이와 같이 우리는 오직 같은 기술에 의한 파우더 형태로 측정하여 비교 할 수 밖에 없다. 이것은 모래알 같은 입자는 표준 크기로서 어떤 것도 할 수 없음을 의미한다. 표준은 각 기술들 사이의 비교를 통해 구형이어야만 한다. 그러나 우리는 각각의 기술로서 표준 입자 크기를 얻을 수 있고 이것은
기술을 사용한 장비의 비교를 하게 될 것이다. 

 

 

D[4,3]

 

1,2,3 단위의 치수인 3 가지 구가 있다고 생각해보자. 세 입자 사이의 평균 크기는 어떻게 될 것인가? 처음에 우리는 아마 2 라고 말할 것이다 .어떻게 이 답을 얻었을까?  


우리는 모든 값을 더하고 총 입자수로 나눌 것이다.    

 

 

 

이것은 수 평균이다(더 정확하게는 길이 평균의 수이다). 입자의 수는 방정식으로 나타낼 수 있다.  

 

 

 


수학적인 용어로 D[1,0] 으로 불린다.  

이유는 위에 방정식의 diameter 항은 (d1)양이 많고 밑의 방정식은 diameter 항(d0)이 없다. 그러나 내가 촉매관련 공학도라고 생각해보면 표면적에 기초해 이러한 구를 비교하기 원할 것이다. 그 이유는 더 높은 표면적이 더 높은 촉매의 반응성을 가지기 때문이다.  

 

구의 표면적은 이다. 따라서 표면적에 기초하여 비교한다면 우리는 반드시 입자수로 나눈 직경들의 제곱을 구해야 한다. 그리고 평균 직경으로 되돌아 가기 위해서 사각형의 근을 취해야 한다.  

 

 

이것은 다시 수평균이다(표면 수의 평균). 이유는 입자의 수가 밑의 방정식에 나타난다. 우리는 직경의 제곱을 모두 더한다. 그래서 수학적인 용어로 D[2,0]이라고 불린다. – 방정식의 위항은 제곱했고 직경 항은 밑이다. 만약 내가 화학 전공자라면 나는 기본 무게의 구를 비교하기를 원할 것이다. 구의 무게에 대한 식은 다음과 같다. 

 

 

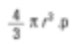
그리고 인자의 수로 나눈 사각형의 치수를 알아야 하고 평균 직경으로 되돌아 가기 위해서 정육면체의 근을 취해야 한다.