폴리머는 2개의 구조적 범주, 즉 선형(linear) 폴리머와 브랜치 (branched) 폴리머로 크게 구분할 수 있다. 선형 폴리머는 꼬리 형태의 끝부분에 규칙적으로 연결된 반복적 단위들의 단일 주사슬로 이루어진다. 반면, 브랜치 폴리머는 형태가 다양하다. 빗살 모양 폴리머(comb polymer)는 주 폴리머 backbone에서 방사되는 비슷한 구조의 brenching를 갖고 있다. brenching의 길이는 매우 다양한데, 랜덤브랜치 폴리머들은 다양한 brenching점을 갖고 있어서 backbone 뿐만 아니라 brenching에도 결합되어 있다. 덴드리머(dendrimer) 라고도 불리는 별모양(starburst) 폴리머는 핵심부에서 시작된 대칭적 brenching들이 중심에서 바깥쪽으로 방사하는 모양이다. 이러한 구조들은 그림 1의 개념도에 제시되어 있다.
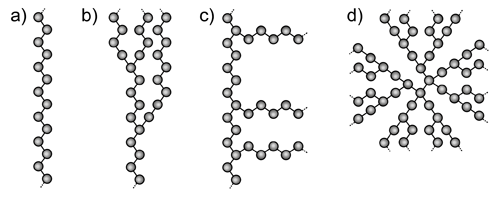
|
호모 폴리머의 분자량 분포는 알려진 표준의 용리 프로필을 미확인 폴리머의 용리 프로필과 비교함으로서 크기 배제/겔 침투 크로마토 그래피(SEC/GPC)를 사용하여 일상적 으로 특성화할 수 있다. 소위 컬럼 보정이라고 불리는 접근법의 적용은 크로마토그램 각각의 조각에 대한 절대 분자량 측정을 위해 농도 검출기(RI 또는 UV)와 광산란 검출기 를 통합하는 Viscotek TDAmax 등 고급 다중 검출 SEC 시스템을 사용한다면 피할 수 있다. 폴리머의 고유점도 측정을 원활하게 하기 위해 브리지 점도계도 포함된다. 블록 코폴리머 조성의 경우, 두 번째 농도 검출기가 추가된다. 하나는 요소 B의 양을 측정하기 위한 것이고 다른 하나는 A + B의 양을 측정하기 위한 것이다.
다중 검출 SEC 시스템에 포함된 각각의 고유한 검출기에 관련된 ‘특정적 특성 측정 능력’과는 별개로, 서로 다른 검출기에서 발생한 신호들의 결합을 통해 추가적인 정보를 얻을 수 있다. 예를 들어, 점도계 검출기에서 얻은 고유점도를 광산란 검출기에서 얻은 폴리머량과 결합(연계)하면 수력학적 반경 (DLS에 의해 측정된 반경에 상응함)의 계산이 용이해진다. 폴리머 brenching는 광산란 검출기를 고유 점도 검출기와 결합하여 파악할 수 있는 또 다른 탄젠트 특성이다.
2개의 Viscogel 컬럼이 탑재된 Viscotek TDAmax 시스템을 사용하여 4개의 합성 코폴리머 시료의 특징을 규명했다. 첫 번째 시료는 선형 코폴리머였다. 나머지 3개의 시료들은 랜덤으로 브랜치 코폴리머들로서, 낮은 수준의 brenching(low-brch), 중간 수준의 brenching(Mid-brch), 높은 수준의 brenching(High-brch)로 라벨 표시를 했다. 시료들은 1mL/min의 유속으로 작동되는 GPC 시스템을 통해 THF 용액에서 용리되었다. 각 코폴리머의 분자량, 폴리머 고유 점도, 스톡스 반경은 Viscotek OmniSEC을 통해 직접 계산되었다. 평균 brenching와 brenching 빈도는 Zimm-Stockmayer 방정식을 사용하여 OmniSEC를 통해 계산되었다.
|
|
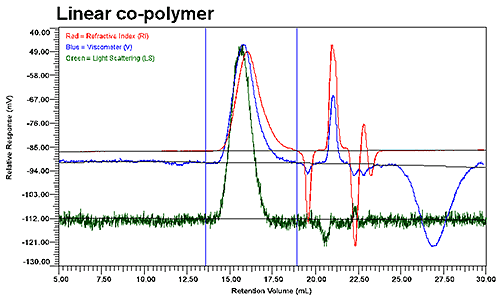
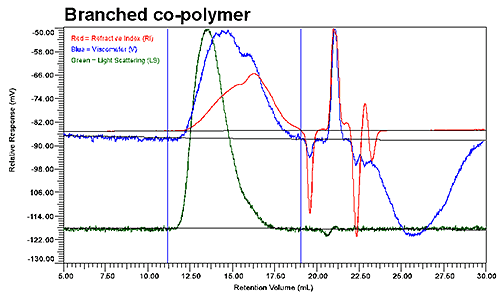
그림 2는 선형 코폴리머 및 저brenching 코폴리머 시료들에 대한 GPC 결과를 보여준다. 이 그래프에는 UV 신호가 제시되지 않았음에도 불구하고, UV 신호는 코폴리머의 분포를 통틀어 폴리머 조성 검증을 위해 사용되었다. 그림 2에 제시된 2개의 크로마토그램에서 분명히 볼 수 있듯, 선형적 코폴리머들과 브랜치 코폴리머들의 용리 프로필은 크게 다른데, 점도 및 굴절률 검출기는 두 개의 모집단들이 브랜치 코폴리머에 대한 적분한계 내에 있음을 나타내지만 선형 코폴리머에 대해서는 오직 한 개의 모집단만이 그러하다.
| 시료 ID | Mn (Da) | Mw (Da) | Mw/Mn | [η] (dL/g) | dñ/dC (cm3/g) | RH (nm) |
|---|---|---|---|---|---|---|
| 선형 | 4838 | 14488 | 2.99 | 0.0927 | 0.083 | 2.60 |
| Low-brch | 5158 | 87918 | 17.0 | 0.1080 | 0.083 | 4.47 |
| Mid-brch | 4168 | 84264 | 20.2 | 0.0953 | 0.092 | 4.07 |
| High-brch | 6159 | 79075 | 12.8 | 0.0946 | 0.093 | 4.12 |
표 1은 중량(Mw), 갯수(Mn) 평균 분자량, 다분산(Mw/Mn), 고유점도 ([η]), 굴절률 증가 (dñ/dC), 수력학적 반경(RH)을 포함하여, TDAmax 시스템을 통해 측정하고 계산한 폴리머의 표준 특성을 보여준다.
표 1에서 선형 폴리머는 ‘브랜치 폴리머’에 비해 분자량과 다분산이 훨씬 더 작음을 보여준다. 이러한 사실에도 불구하고 모든 4개의 시료에 대한 고유점도는 비슷한데, 이러한 우연의 일치는 분자량에 대한 크기의 비율이 모든 시료에 대하여 거의 일정하기 때문이다. dñ/dC 값은 굴절률 신호 및 확인된 주입 질량으로부터 계산되며 코폴리머 조성을 나타낸다. 표 1에서 볼 수 있는 것처럼, 선형 및 저brenching 코폴리머들은 동일한 dñ/dC 값을 갖는다. brenching의 정도가 증가하면 측정된 dñ/dC 값도 증가한다. 이러한 경향은 brenching를 선호 하는 코폴리머의 조성에 차이가 있음을 반영한다.
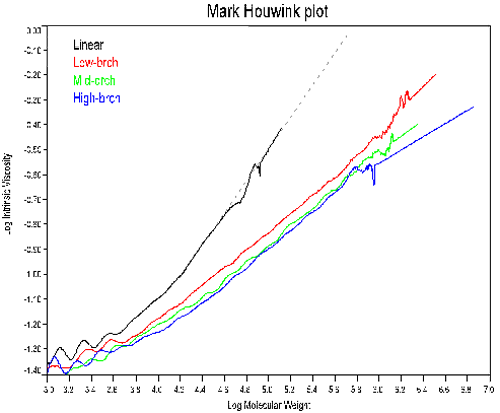
brenching의 정도를 측정하기 위해, 선형 구조를 가진 동일한 폴리머를 확보하거나 선형 폴리머에 대한 Mark-Houwink 매개변수(K와 a)를 확인해야 한다. 그림 3은 4개의 코폴리머에 대한 Mark-Houwink 도식을 보여준다. 선형적 시료는 K와 a를 파악하기 위해서 사용되었다.
|
그림 3에서 볼 수 있는 것처럼, Mark-Houwink의 기울기는 폴리머 brenching가 증가함에 따라 감소한다. 이러한 경향은 brenching에 대한 dñ/dC의 의존과 유사한데, 이는 brenching에 대한 조성의 영향을 나타낸다. 분자량이 일정할 때, brenching이 증가하면 크기가 감소하고 이후에는 고유점도가 감소한다. 그러므로 그림 3에 제시된 감소하는 기울기는 예상되지 않는다. 그림 3에서 볼 수 있는 선형 폴리머에 대한 추세선은 brenching의 계산을 위해 예상되는 고유 점도값을 추정하기 위해 사용되었다.
폴리머 시료들에 대한 brenching 매개변수 계산을 위한 첫 번째 단계는 선형 폴리머 고유점도([η])에 대한 브랜치 폴리머 고유점도의 비율인 g‘의 분자량 의존을 계산하는 것이다.
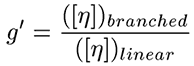
|
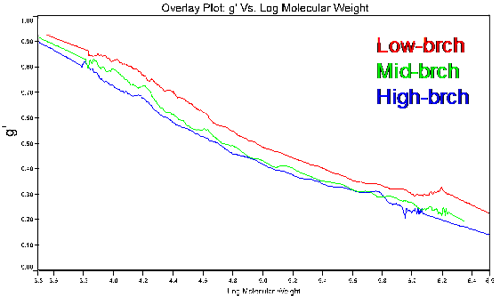
그림 4는 본 연구에서 브랜치 폴리머에 대한 수축 인수 g’.의 분자량 의존을 도식화했다. 이 그림에서는 두 brenching를 관찰할 수 있다. 첫째, 일반적으로 맨 위에서는 brenching의 정도가 낮고 맨 아래에서는 brenching의 정도가 높으며, 모두 저분자량의 한계 내에 있는 1로 수렴된다. brenching가 증가하면 점도가 증가하고 이후에는 g’.가 감소하므로, 이러한 관찰은 예상과 일치한다. 저분자량의 한계에서, brenching량은 0이 되기 때문에 저MW의 한계 내에서 g’ = 1로 수렴된다. 중요한 두 번째 관찰 결과는 중brenching 및 고brenching g’ 결과는 폴리머의 화학적 생성 방식에 따라 더 높은 분자량에서 수렴되는데, 분자량이 더 높을 때 brenching가 증가하는 것이다.
|
폴리머 시료들에 대한 brenching 매개변수 계산을 위한 두 번째 단계는 선형 폴리머의 회전반경Rg에 대한 브랜치 폴리머의 회전반경(Rg)의 제곱인 g를 파악하는 것이다. 동적 광산란 점도 측정에서 도출되는 수력학적 반경(RH,)과 혼동을 피하기 위해, 회전반경은 각도 의존적 정적 광산란 측정에서 도출된 반경의 제곱평균이다. 이러한 예를 포함하여 많은 경우, 작은 분자들에서 산란된 빛의 각도 의존이 없으므로 Rg를 파악하는 것은 불가능하다. Rg정보가 없는 경우, g는 아래 식에 제시된 것처럼 구조 인자 B를 이용해서 g’로부터 파악될 수 있다. 브랜치 폴리머 체계의 경우, B의 범위는 저brenching에 대해서는 0.5이고 고brenching에 대해서는 1.5인데, 중brenching 체계는 0.75의 B 값을 갖는다.
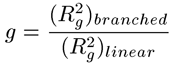
|
With
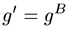
|
이때 g' = gB 폴리머 시료들에 대한 brenching 매개변수의 파악을 위한 마지막 단계는 적합한 Zimm-Stockmayer 식을 사용하여 확인된 g 값으로부터 brenching 횟수와 빈도를 계산하는 것이다. Zimm-Stockmayer 방정식은 폴리머 형태(예: 별모양, 선형 등), 다분산, 수축 인자 g에 대한 brenching횟수에 관련된 brenching점 의존적 방정식별 암의 개수로 구성된다. 본 연구에서 특징이 규명된 코폴리머들은 다분산, 랜덤, 삼중활성 폴리머들이다. 이러한 유형의 폴리머 에 대한 Zimm-Stockmayer 방정식은 아래와 같으며, 여기에서 nw는 brenching 횟수이다.
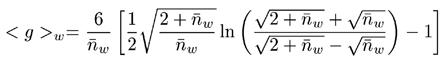
|
brenching 빈도( )는 다음과 같은 방정식을 통해 파악될 수 있는데, 여기에서 Mi은 각각의 크로마토그래피 조각에 대한 질량이고 FR은 100 반복 단위의 질량으로 정의된 반복 인수이다.
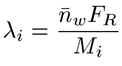
|
|
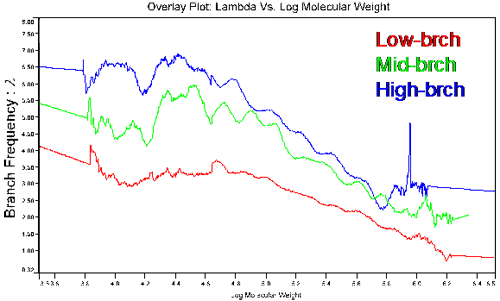
그림 5는 본 연구에서 특징이 규명된 3개의 코폴리머에 대한 brenching 빈도의 분자량 의존을 보여준다. 이 그림에서는 3개의 폴리머들 간의 차이가 뚜렷한데, 지금까지 제시된 가장 대조적인 결과를 보여준다. [η]와 g’ 그림 내의 더 높은 분자량에서 수렴되는 경향이 있는 중/고 브랜치 폴리머들의 brenching 빈도는 서로 뚜렷하게 다르다.
| 시료 ID | Branches | Branch Freq. |
|---|---|---|
| 선형 | 0 | 0 |
| Low-brch | 17.8 | 2.68 |
| Mid-brch | {26.2} | 3.82 |
| High-brch | {29.2} | 4.99 |
표 2는 brenching들의 평균 개수(nw)와 중량 평균 brenching 빈도(λ)를 나타낸다. nw 및 λ 는 둘 다 각각의 분자량에서 brenching된 시료의 점도를 선형 시료의 점도에 비교해서 계산되었다. 저brenching의 예상빈도는 가장 낮은 수준인 2.68였던 반면, 고brenching의 경우에는 가장 높았고 brenching 빈도가 100개의 반복 단위 당 5개 brenching점에 근접했다. g’ 대(對) 분자량의 그래프는 3개 시료들에서 큰 편차를 보이지 않았음에도 불구하고 brenching 빈도에 대한 결과적인 값들은 큰 편차를 보였는데, 이는 이 매개 변수의 민감도를 보여주는 것이다.
Samples provided by Dr. Robert Hunter of Unilever Research and Strathclyde University
Modern Methods of Polymer Characterization, H. G. Barth, J. W. Mays Eds. Wiley-Interscience, 1991. Chapter 3, "Measurement of long-chain branch frequency in synthetic polymers" A. Rudin
Structural Characterization of Polymers in Solution by Quasielastic Laser Light Scattering, A.M. Jamieson and M.E. McDonnell, Probing Polymer Structures; Am. Chem. Soc. Adv. Chem. Ser. 174, p. 163, American Chemical Society, Washington, DC., 1979
Light-scattering Characterization of the Molecular Weight Distributions of Some Intractable Polymers, C. Wu, Polym. For Adv. Tech. 8, p. 177.

|
Viscotek TDAmax는 완전한 크기 배제적 크로마그래피(SEC) 시스템 이며, 광산란, 점도계, 차굴절계(RI) 검출기들을 포함하여, 결합형 자동 시료주입장치, 펌프,가스 제거기 (GPCmax), 열제어 컬럼 구획, 3중 검출기 어레이를 통합한다.
시스템 제어, 데이터 수집 및 크로마토그래피 분석 기능은 Viscotek OmniSEC 소프트웨어가 제공하는 하나의 완전한 패키지로 제공된다.