액체 중 부유하거나 분산된 입자 또는 액적 물질은 여러 산업에서 다양한 용도로 사용되고 있습니다. 액체 연마제, 세라믹, 약품, 식품류 및 잉크 등이 여기에 포함됩니다. 이 응용 분야 전반에 걸쳐 가장 중요한 기준은 현탁액의 안정성입니다. 현탁액이 기능성을 갖기 위해서는 제품의 수명이 끝나기 전까지 일정한 분산상을 유지하거나 침전이 일어났을 때 쉽게 다시 분산될 수 있어야 합니다. 분산된 상의 안정성에 기여하는 여러 요소가 있으며 이것들은 열역학적 또는 운동 역학적 방식으로 작용합니다. 전자(열역학적 요소)는 입자의 반발력을 통해 안정화를 유도하는 입체적 또는 정전기전 안정화를 유도하며, 부유 매체의 점도를 증가시켜 응집 및 침강속도를 늦추는 운동역학적 방식으로 안정성을 유도할 수도 있습니다.
서브마이크론의 현탁 입자의 브라운 운동은 입자들의 분산상을 유지하는데 매우 중요하지만 분산상과 연속상의 밀도차이가 있는 경우 큰 입자는 중력의 영향을 더 클 수 있습니다. 이런 경우에는 브라운 힘에 대한 중력의 비를 방정식 1에 대입하여 침전의 가능성을 예측할 수 있습니다[1].
(1)

|
여기서 a는 입자 반경, Δρ는 분산상과 연속상 간의 밀도 차이, g는 중력으로 인한 가속도, kB는 볼츠만 상수, T는 온도입니다. 이 비율이 일정 수준보다 높으면 어느 정도의 침전이 예상되며, 비율이 일정 수준보다 낮으면 시스템이 안정적일 가능성이 높습니다. 그러나 이 방정식에서는 입자 간의 잠재적 상호작용은 고려하지 않습니다. 브라운 운동으로 인해 입자들은 서로 끊임 없이 충돌하며, 결국 반데르 발스 인력으로 인해 응집될 수 있습니다. 이로 인해 훨씬 크기가 큰 이차 입자(플록)가 형성될 수 있으므로 이후의 침강을 고려하면 방정식 1에서 중력의 기여도가 더 큽니다.
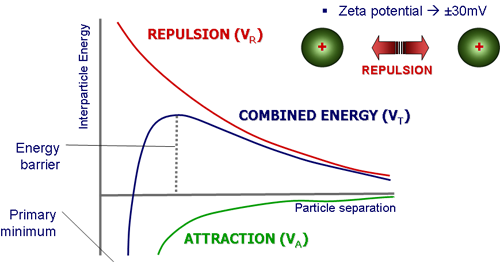
입자들이 응집되는 것을 막으려면 어떤 장벽을 만들어야 합니다. 중합체를 흡수하거나 pH를 바꾸거나 하는 방식으로 입자 표면이 전하를 띠게 하는 등의 입체적이거나 정전기적인 수단으로 장벽을 만들 수 있습니다. 반발력이 인력보다 크면 안정적인 시스템이 만들어집니다. 전하를 띤 현탁액의 경우, 그림 1a와 같이 복합/총 에너지(VT)는 인력(VA)과 반발력(VR)의 합이라는 DLVO 이론으로 힘의 균형이 설명됩니다. 이 이론은 두 입자가 서로 접근할 때 충분한 열에너지를 갖고 있지 않다면 반발력에 의해 형성된 에너지 장벽을 극복하지 못해 서로 들러붙는 것을 방지한다고 주장하고 있습니다. 이 전위 장벽의 크기는 용매로 둘러 싸인 입자와 이중층 사이에 형성된 미끄럼 면의 전위인 제타 전위의 크기로 나타낼 수 있습니다[4, 5]. 현탁액에 있는 모든 입자가 큰 음전하 혹은 양전하의 제타 전위를 가지고 있을 때 서로 간의 반발력이 더 커지는 경향을 보이며 서로 결합하려 하지 않습니다. 그러나 낮은 제타 전위를 가지게 되면 입자들은 반발력이 충분하지 않아 결국 응집이 일어나게 됩니다. 안정적인 현탁액과 불안정한 현탁액을 나누는 일반적인 기준은 +30 또는 -30mV로서 이 이상의 제타 전위를 가진 입자는 보통 안정적인 것으로 간주됩니다[6, 7]. 그러나 이는 입자 특성에 따라 크게 달라집니다[1, 4]. 본 자료에서는 침강 현상과 관련하여 입자의 크기, 제타 전위 및 유변학적 특징의 중요성을 설명하고 이러한 입자 특성을 조절하여 안정성을 높이는 방법을 소개합니다.
|
|
본 연구에 사용된 샘플은 Hydro S를 분산 장치를 장착한 Malvern Mastersizer 2000으로 측정한 밀도 2.6g/cm3, Dv(50) 3.7μm의 미정질 이산화규소입니다. 제타 전위 측정 및 꾸준한 전단 유변학적 측정을 통해 샘플을 분석함으로써 pH 값과 안정성의 함수 관계를 파악하였습니다. 제타 전위 측정에서는 MPT-2 자동 적정기와 함께 Malvern Zetasizer Nano ZS를 이용한 분석을 위해 정제수로 물질을 희석하고 분산시켰습니다. 적정에는 0.25M과 0.025M HCl을 사용하였으며 시작/샘플 pH에서 pH 1.0까지 적정하고 해당 범위를 10등분하여 제타 전위를 3회 반복 측정하였습니다. 모든 시험은 25ºC에서 실시되었습니다.
유변학적 측정은 정제수 내 농축 실리카 시료 분산액(75% w/w)에서 진행되었습니다. 제타 전위 시험에 사용된 것과 동일한 pH 조건을 만들기 위해 시료의 전해질 농도를 HCl로 조절하였습니다. 톱니 모양의 평행 플레이트와 0.5mm의 작동 간극을 사용하는 Kinexus Pro 및 Gemini 2 레오미터로 유변학적 시험을 실시하였습니다. 평형 단계적 전단 속도 시험과 전단 응력 램프 시험 등 두 가지 시험이 이루어졌습니다. 첫 번째 시험에서는 전단 속도를 0.1에서 100s-1로 단계적으로 높여 흐름 곡선(전단 속도 대비 전단 점도)을 산출하였습니다. 두 번째 시험에서는 전단 응력을 60초 동안 선형적으로 0에서 100Pa까지 끌어올려 항복 응력을 측정하였습니다. 모든 시험은 25ºC에서 실시되었습니다.
그림 2는 정제수에 분산된 실리카 입자에 대한 pH의 영향을 보여주는 것으로 Mastersizer 2000을 이용하여 측정한 평균 입자 크기는 3.7μm였습니다. 30mV를 초과하는 음의 제타 전위를 가지고 있음에도 불구하고 이 현탁액은 비활성 상태에서 조밀한 침전층을 형성하며 불안정한 분산 형태를 보였습니다. 방정식 1에 관련 입자/유동 매개 변수를 대입하면 브라운 힘 대비 중력 비는 45를 초과하는 것으로 나옵니다. 이는 중력의 영향이 결정적으로 작용하며 제타 전위가 침전 안정성에 유의한 영향을 미치지 않을 가능성이 높음을 시사합니다. 동일한 방정식에서 브라운 힘은 직경 1.5μm 미만의 입자에 대해서만 결정적인 영향을 미쳤습니다. 입자 크기와 밀도에 의해 유도된 중력이 시스템에 결정적인 영향을 줄 경우, 정전기적 상호작용은 안정성을 유지하는 데 충분하지 않으며 다른 안정화 수단이 필요합니다.

|
한 가지 방법은 침강 속도를 늦추어 현탁액의 운동역학적 안정성을 높이는 것입니다. 이는 연속상의 점도를 높임으로써 가능합니다. 침강 속도는 희석된 현탁액이 구 형태의 입자로 구성되어 있다는 가정하에 스토크스의 법칙(Stokes' law)(방정식 2)을 이용하여 추정할 수 있습니다[2].
(2)

|
여기서 V는 침강 속도이고 η는 연속 상(phase)의 전단 점도입니다. 점도가 두 배 높아지면 침강 속도도 두 배로 낮아지는 반면 입자 크기가 절반으로 줄어들면 침강 속도는 4배 느려집니다. 그러나 이 수식은 입자의 상호작용이 최소화된 묽은 현탁액에만 적용할 수 있습니다. 이웃한 입자들 간의 상호작용과 입자 부하가 높으면 전체적인 밀도와 점도가 높아지기 때문에 농축된 현탁액의 침강은 더욱 복잡한 문제입니다. 농축 현탁액의 침전 속도를 예측하는 방정식은 여러 개가 있으며 그 중 하나는 스토스크 방정식을 수정한 것(방정식 3)으로 φ는 체적 비율을 나타내고 지수는 입자 크기에 따라 달라지는데 1μm보다 큰 입자에 대해서는 약 5.25, 마이크론 미만의 입자에 대해서는 4.75입니다[2].
(3)

|
입자 전하 역시 침강 속도를 늦추는 데 중요한 역할을 할 수 있는데, 이것은 관련된 정전기층이 분산상의 유효 위상 체적을 높이는 유한 두께를 가지기 때문입니다. 입자의 크기가 작을수록 이러한 효과는 더욱 뚜렷해집니다[1, 2].
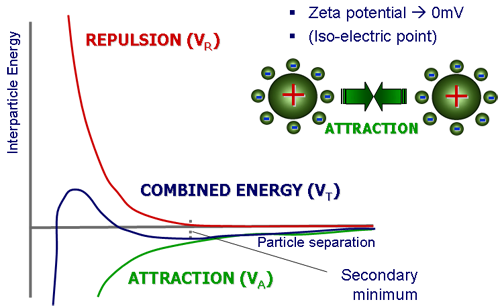
중력의 영향이 결정적인 현탁액의 안정성을 유도하는 또 다른 방법은 망상 구조를 만들어 시스템에 항복 응력을 가하는 것입니다. 적절한 첨가제를 사용하여 연속상을 겔화하는 방법이 있습니다. 직관적으로 보일 수 있는 또 다른 방법은 입자들 간의 반발력을 낮추고 그림 1b에서 보듯이 시스템 내의 응집을 촉진하는 것입니다. 후자에 대해서는 보다 자세히 다룰 것입니다.
그림 2에서 pH를 낮추면 제타 전위가 낮아지며 pH1.17에서 등전점이 나타나는 것을 알 수 있습니다. 그림 3은 이러한 변화가 다양한 샘플에 대하여 전단 속도와 전단 점도의 함수 관계 등의 유변학적 측면에 미치는 영향을 나타내었습니다. pH 3.9에서 점도가 상당히 낮아지고 전단 속도가 증가함에 따라 점도가 약간 낮아지는 것은 비뉴턴 또는 shear thining한 거동의 지표입니다. 낮은 전단 속도에서 약간 높은 값에서 안정화된 점도는 영의 전단 점도(zero shear viscosity) 안정화로 간주되며, 낮은 전단 속도에서는 입자들의 불규칙한 배열과 입자들의 전하로 인한 유효 위상 체적의 증가로 인해 발생합니다. 보다 높은 전단 속도에서는 유체역학적 요소의 영향이 지배적이기 때문에 분산상 배열의 규칙성이 높아지고 이로 인해 점도가 감소합니다[1].

|
pH가 낮아지면 점도는 높아지고 낮은 전단 점도에서 안정화되는 것을 더 이상 눈으로 관찰할 수 없습니다. 이러한 전단 안정화(shear plateau)가 없다면 해당 물질이 고체적 거동을 보이고 있음을 추론할 수 있습니다. 하지만 이를 확신하려면 더 낮은 전단 속도 측정값이 필요합니다. 미리 전단된 샘플에서 동일한 시험을 반복한 결과 모든 경우에 거의 동일한 흐름 곡선이 관찰되었으며, 이는 샘플이 영구적으로 엉기는 것이 아니라 작은 변화에도 형태가 바뀌는 일시적인 망상 구조를 가지고 있음을 의미합니다. 이는 낮은 전단 속도에서의 점도를 측정한 다음 일정 시간 동안 높은 전단 속도에서 전단된 후 점도를 회복하는 데 걸린 시간을 측정한 3단계 전단 속도 시험을 통해 다시 확인되었습니다. 시작과 종료 전단 속도 0.1s-1, 중간 전단 속도 10s-1을 이용하여 pH 4에서 시험한 샘플의 시험 결과가 그림 4에 나와 있습니다. 이는 샘플의 점도가 거의 바로 회복되었음을 나타내며 처음 관찰한 것에 비해 점도가 약간 높아진 것은 미세 구조의 재구조화로 인한 것으로 보입니다.

|
이러한 가역적 엉김 현상은 DLVO 이론으로 설명할 수 있습니다. 입자의 표면 전하가 낮아지면 총 상호작용 전위에서 반발력의 기여도가 줄어듭니다. 이로 인해 그림 1b에서 보듯이 전위 에너지 곡선에 이차 최소점이 나타나며 입자들 간에 훨씬 약하고 가역적인 응집이 가능해집니다. 이러한 상호작용은 브라운 운동의 영향을 견딜 만큼 충분히 강하면서도 전단력 하에서 파괴될 만큼은 충분히 약합니다. 이차 최소점의 깊이는 플록 구조를 파악하고 망 구조의 전위를 측정하는 데 있어 핵심적인 역할을 합니다. 이차 최소점이 10 ~ 20kT 정도로 깊으면 충돌하는 입자들이 강하게 접착되어 망상 구조에 적합하도록 위상 체적이 큰 개방형 구조를 형성합니다. 이와 반대로 약하게 엉겨있는 시스템은 부분적으로 재배열이 일어나 높은 밀도의 플록을 형성하여 쉽게 침강됩니다[1, 2].
이 망상 구조의 강도는 인력을 극복하고 흐름이 시작되는데 필요한 항복 응력에 반영될 수 있습니다. 레오미터에서 항복 응력을 측정하는 시험의 종류는 많습니다. 가장 빠르고 쉬운 방법 중 하나는 전단 응력 스위프(shear stress sweep)를 실시하고 점도가 가장 높은 지점의 응력을 측정하는 것입니다. 피크에 도달하기 전에 관찰되는 점도 증가는 탄성 변형(변형 경화)의 결과이므로 피크 값은 탄성 구조가 무너지는 지점을 나타냅니다.
그림 5에서 두 개의 낮은 pH에서 샘플의 항복 응력 지표인 점도 피크를 확인 할 수 있습니다. 또한 이 피크 지점의 응력은 pH가 낮은 샘플에서 훨씬 높은데 이는 제타 전위가 낮아지면서 구조적 강도가 높아짐을 의미합니다. pH가 높은 샘플의 경우에는 점도 피크가 없는데 이는 이 물질이 항복 응력을 가지고 있지 않아 망상 구조가 없음을 의미합니다. 이 경우에 방정식 3을 통해 침강속도를 추정할 수 있으며, 미립자 겔의 열역학적 안정화는 구조에 가해진 응력이 항복 응력보다 낮을 때 이루어집니다. 입자가 주변에 부과한 응력은 방정식 4를 통해 추정할 수 있습니다. ρD는 분산상의 밀도, ρC는 연속상의 밀도를 나타냅니다.

|
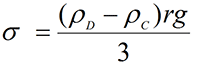
|
이 연구에서 사용된 실리카 현탁액에서 가장 큰 입자(직경 약 10μm)의 계산값은 약 0.01Pa이었습니다. 따라서 pH가 낮은 시스템에서 잠잠한 상태에서는 침강에 안정적이지만 운송 중에 발생하는 충격 등 외부의 변화로 인해 발생하는 응력 또한 고려가 필요합니다.
[1] Larson, R.G (1999), The Structure and Rheology of Complex Fluids, Oxford University Press, New York.
[2] Barnes, H.A (2000), A Handbook of Elementary Rheology, University of Wales, Institute of Non-Newtonian Fluid Mechanics.
[3] Hunter, R.J (1988), Zeta Potential in Colloid Science: Principles and Applications, Academic Press, UK.
[4] B. Derjaguin, L. Landau (1941) Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes, Acta Physico Chemica URSS 14, 633.
[5] E.J.W. Verwey and J. Th. G. Overbeek (1948) Theory of the stability of lyophobic colloids, Elsevier, Amsterdam.
[6] Zeta Potential in 30 Minutes, Technical Note available from www.malvern.com
[7] Zeta Potential of Colloids in Water and Waste Water, ASTM Standard D 4187-82, American Society for Testing and Materials, 1985