이것을 묻는 것은 아주 어리석은 질문이다. 하지만 다양한 입자 크기 분석 기술에 있어서 이러한 것은 기초가 된다. 분산 과정과 재료의 모양은 입자 크기 분석에 있어 처음보다 더욱 복잡해진다.
성냥갑을 주고 누군가가 이 성냥갑의 사이즈가 얼마인지 말해보라고 물었다고 가정해보자. 아마도 이 성냥갑의 크기가 20*10*5mm 라고 대답할 것이다. “성냥갑의 크기가 20mm”라고 정확하게 대답할 수 없을 것이고, 이러한 것은 크기를 말하는데 하나의 견해일 것이다. 그래서 당신은 한 개의 고유 치수로는 3 차원으로 된 성냥갑을 묘사 할 수 없다.
명백하게 이러한 상황은 모래의 입자나 페인트 깡통 안의 색소입자와 같은 복잡한 모양에서는 더욱 어려워진다. 내가 만약 Q.A.(품질관리) 매니저라면, 입자를 묘사하는데 하나의 숫자가 원할 것이다 - 예를 들어 마지막으로 만들어진 제품의 평균 크기가 증가되었는지 감소되었는지 알기를 원할 것이다. 이것은 입자 크기 분석문제에 기본적인 문제이다. - 어떻게 우리는 오직 하나의 숫자로 3 차원적인 물체를 표현할까?

|
하나의 유일한 숫자로 표현 가능한 구가 있다 만약 우리가 50μm 크기인 하나의 구를 말할 때 이것은 정확하게 표현 가능하다. 50μm 크기 큐브의 모서리와 대각선을 말할 때는 표현을 할 수 없다. 많은 특징이 있는 성냥갑은 하나의 숫자로 표현 가능하다. 예를 들면 부피와 표면적에 관련한 무게는 하나의 특정한 수이다. 그렇다면 만약 성냥갑의 무게를 측정하는 기술이 있다면 우리는 성냥갑의 무게를 구의 무게로 변환할 수 있다. 기억해야 할 것은
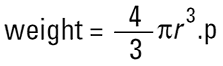
|
그리고 성냥갑과 같은 무게의 구의 직경에 대한 하나의 특정수(2r)를 계산한다. 이것이 equivalent sphere 이론이다. 우리는 어떤 입자의 성질을 측정하고 구라고 언급한 입자를 가정한다. 그러므로 입자를 표현하기 위한 하나의 특정한 수(구의 직경)로 얻는다.
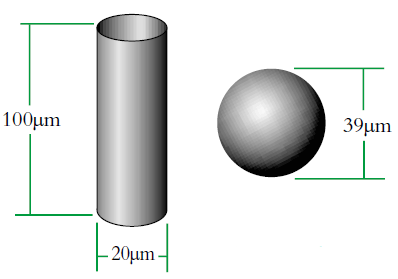
이것은 3 차원입자를 표현할 때 비록 제어 목적을 위해 더 정확한 것은 불편할지 모르지만 3 또는 그 이상의 수로서 표현할 필요가 없다는 것을 말해준다. 2). 이것이 물체의 모양에 의존하는 흥미로운 효과들을 알 수 있고 예로써 구와 같은 실린더를 도시하였다. 그러나 만약 실린더의 모양이나 크기가 변한다면 부피/무게는 달라질 것이다. 그리고 등가 구형 모델로서 우리는 최소한 그것은 더 작아지거나 커졌다고 말할 수 있다.
|
실린더의 직경이 D1=20μm 높이 100μm 이라고 생각해보자.
직경이 실린더와 부피가 같은 D2 의 직경을 가진 구가 있다. 우리는 다음과 같이 직경을 계산할 수 있다.
실린더의 부피 =
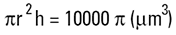
|
구의 부피 =
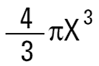
|
X 는 부피 반경 값이다.
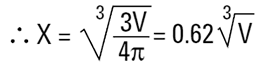
|
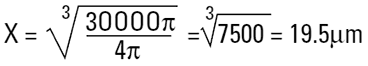
|
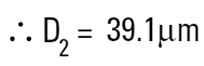
|
100μm 높이와 20μm 직경의 실린더의 구형직경의 부피는 대략 40μm 이다. 밑의 표는 다양한 비율의 실린더의 구형의 직경을 나태내고 있다. 마지막 줄은 전형적인 디스크모양의 큰 클레이 입자일 것이다. 그것은 높이 20μm 에 0.2μm 의 두께를 가지기 때문에 일반적으로 차원을 고려하지 않아도 될 것이다. 입자의 부피를 측정하는 도구에 관해 우리는 약 5μm 정도에서 답을 얻을지도 모른다. 따라서 이러한 답에 이의를 제기할 가능성에 대해 다른 기술을 사용해야 한다.
또한 이러한 모든 실린더들은 25μm 인 여과기와 같은 사이즈로 나타날 수 있는데 이때 “모든 물질은 25μm 보다 작다”고 말할 수 있다. 이러한 실린더들은 각각 다른 값을 가지고 있으므로 레이저 회절 시 다르게 보여질 수 있다
| Size of cylinder | Aspect Ratio | Equivalent Sperical Diameter | |
|---|---|---|---|
| Height | Diam. | ||
| 20 | 20 | 1 1 | 22.9 |
| 40 | 20 | 2:1 | 28.8 |
| 100 | 20 | 5:1 | 39.1 |
| 200 | 20 | 10:1 | 49.3 |
| 400 | 20 | 20:1 | 62.1 |
| 10 | 20 | >0.5:1 | 18.2 |
| 4 | 20 | 0.2:1 | 13.4 |
| 2 | 20 | 0.1:1 | 10.6 |
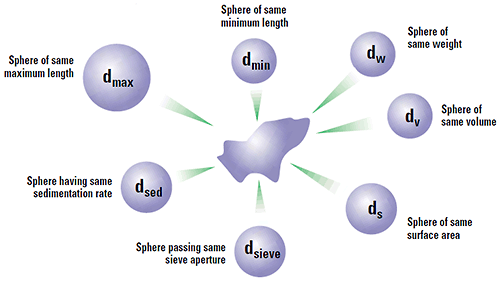
명백하게, 만약 현미경을 통해 입자를 보게 된다면 2 차원으로 투사된 것을 볼 수 있고, 입자를 특징화하여 측정할 수 있는 입자의 직경들이 있다. 만약 우리가 입자의 최대길이를 받아들이고 이것을 우리의 크기로서 사용한다면 우리는 입자가 최대 차원을 가지는 구입자라고 말할 수 있다. 마찬가지로 만약 우리가 최소 직경이나 Feter's diameter 와 같은 양을 사용한다면 이것은 우리에게 입자의 크기에 관해 또 다른 답을 제공해 줄 것이다. 이 때문에 우리는 각각의 기술은 입자의 다른 물성(최대 길이, 최소 길이, 부피, 표면적 등)을 측정할 수 있다는 것을 반드시 알아야 한다. Fig 3 은 하나의 모래알을 표현 가능하게 하는 다른 몇몇의 해답들을 나타낸다. 각 기술은 잘못되지 않았다 - 기술들은 모두 옳고 입자의 다른 성질을 측정하는 것이다. 그것은 cm 나 inch 법으로 성냥갑을 측정하는 것이다(당신은 길이를 측정하고 나는 폭을 측정한다!). 이와 같이 우리는 오직 같은 기술에 의한 파우더 형태로 측정하여 비교 할 수 밖에 없다.
|
이것은 모래알 같은 입자는 표준 크기로서 어떤 것도 할 수 없음을 의미한다. 표준은 각 기술들 사이의 비교를 통해 구형이어야만 한다. 그러나 우리는 각각의 기술로서 표준 입자 크기를 얻을 수 있고 이것은 기술을 사용한 장비의 비교를 하게 될 것이다.
1,2,3 단위의 치수인 3 가지 구가 있다고 생각해보자 세 입자 사이의 평균 크기는 어떻게 될 것인가? 처음에 우리는 아마 2 라고 말할 것이다 . 어떻게 이 답을 얻었을까? 우리는 모든 값을 더하고
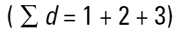
|
총 입자수로 나눌 것이다.(n=3). 이것은 수 평균이다(더 정확하게는 길이 평균의 수이다). 입자의 수는 방정식으로 나타낼 수 있다.
Mean diameter =
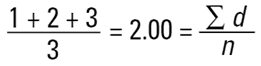
|
수학적인 용어로 D[1,0] 으로 불린다. 이유는 위에 방정식의 diameter 항은 (d1)양이 많고 밑의 방정식은 diameter 항(d0)이 없다. 그러나 내가 촉매관련 공학도라고 생각해보면 표면적에 기초해 이러한 구를 비교하기 원할 것이다. 그 이유는 더 높은 표면적이 더 높은 촉매의 반응성을 가지기 때문이다. 구의 표면적은 4πr2 이다. 따라서 표면적에 기초하여 비교한다면 우리는 반드시 입자수로 나눈 직경들의 제곱을 구해야 한다. 그리고 평균 직경으로 되돌아 가기 위해서 사각형의 근을 취해야 한다.
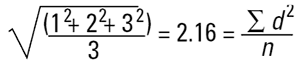
|
이것은 다시 수평균이다(표면 수의 평균). 이유는 입자의 수가 밑의 방정식에 나타난다. 우리는 직경의 제곱을 모두 더한다. 그래서 수학적인 용어로 D[2,0]이라고 불린다. - 방정식의 위항은 제곱했고 직경 항은 밑이다.
만약 내가 화학 전공자라면 나는 기본 무게의 구를 비교하기를 원할 것이다. 구의 무게에 대한 식은 다음과 같다.
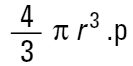
|
그리고 인자의 수로 나눈 사각형의 치수를 알아야 하고 평균 직경으로 되돌아 가기 위해서 정육면체의 근을 취해야 한다.
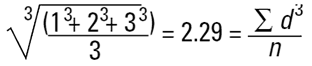
|
다시 이것은 수평균(수-부피 또는 수- 무게 평균)으로 나눈다. 이유는 입자의 수는 방정식으로 나타나가 때문이다. 수학적인 용어로 이것은 D[3,0]으로 표현할 수 있다.
D[1,0],D[2,0],D[3,0] 간단한 평균의 문제는 입자의 수가 공식에 관해 고유하다는 것에 있다. 이것은 많은 수의 입자를 계산할 필요가 일어난다. 계산하는 입자는 오염, 통제, 청결과 같은 적용에서 낮은 수(ppm 또는 ppb) 일 때만 오직 일반적으로 실행된다. 만약 실리카 1g(밀도 2.5)의 크기가 모두 1μm 라면 그것들은 약 760*109 입자가 있다는 간단한 계산으로 나타난다.
따라서 순간 평균 개념은 보충해야 할 필요가 있고 이것은 혼란을 야기할 수 있다.
이러한 평균들은 관성 모멘트와 비슷하고 또 다른 직경에 관련한 선형적인 용어를 소개한다.(아래와 같이 표면적은 d3 와 상관관계가 있고 부피와 질량은 d4 와 상관관계가 있다.)
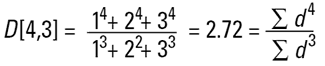
|
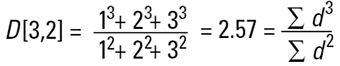
|
이러한 공식은 빈도(표면적 또는 부피/질량)분포의 중심점이 순환하는 것을 나타낸다. 사실상 그것들은 각각의 분포의 중량 중심이다. 이 계산 방법의 장점은 명백하다 - 공식은 입자수를 포함하지 않아서 평균의 계산과 분포는 복잡한 입자의 수에 관한 지식이 필요하지 않다. 레이저 회절은 처음에 부피 항에 기초한 기여를 계산한다. 그리고 이것은 D[4,3]가 뚜렷한 방법으로 보고되어 있기 때문이다.
만약 우리가 직경을 측정하고자 하는 입자를 측정하기 위해서 격자선이 있는 전자 현미경을 사용한다면, 평균의 결과를 얻기 위한 입자수로 나누거나 모두 더한다. 우리는 이 기술에 의하여 수-길이 D[1,0]가 발생하는 것을 볼 수 있다. 만약 우리가 이미지 분석 형식으로 접근한다면 각 입자의 영역은 측정되고 입자의 수로 나눠진다.-D[2,0]이 발생된다. 만약 우리가 전기 장치 같은 기술이 있다면 우리는 각 입자의 부피를 측정할 수 있고 입자 수를 나눌 수 있다 -D[3,0]이 발생된다.
레이저 회절은 D[4,3] 또는 등가부피 평균이 발생할 수 있다. 이것은 만약 밀도가 일정하다면 무게등가 평균은 일치한다.
그래서 각 기술은 다른 평균 직경뿐만 아니라 입자의 다른 성질을 측정하는 것까지 발생 해야 한다. 사람들이 혼란스러운 것은 당연하다! 또한 “옳다“라는 대답과 관련해 무한한 숫자가 있다. 직경이 1,2,3 단위인 3 개의 구가 있다고 가정해보자.
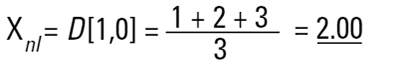
|
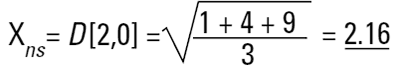
|
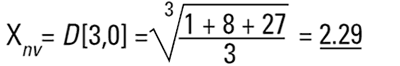
|
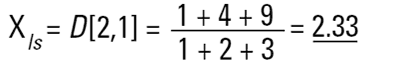
|
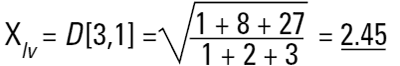
|
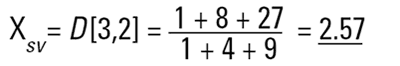
|
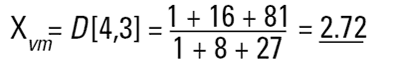
|
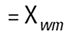
|
| Size(cm) | Number ofObjects | % byNumber | % byMass |
|---|---|---|---|
| 10-1000 | 7000 | 0.2 | 99.96 |
| 1-10 | 17500 | 0.5 | 0.03 |
| 0.1-1.0 | 3500000 | 99.3 | 0.01 |
| Total | 3524500 | 100.00 | 100.00 |
위의 예는 New Scientist (1991 년 10 월 31 일)로부터 나온 것이다. 우주 안에서 지구의 궤도를 도는 것과 그것들의 규칙적인 궤도를 목적으로 사람이 지정한 큰 숫자가 있다. 과학자들은 또한 그것들의 크기를 기초로 해서 그룹을 분류했다.
만약 우리가 위의 세 번째 단락을 조사한다면 우리는 정확하게 모든 입자의 99.3%가 믿을 수 없을 정도로 작다는 것을 추론할 수 있을 것이다. 이것은 숫자를 기본으로 한 data 를 평가하는 것이다. 그러나, 만약 우리가 네 번째 단락을 조사해보면 사실상 모든 물체는 10-1000cm 사이라는 것을 정확하게 추론할 수 있을 것이다. 이것이 모든 물체의 질량이다. 개수와 질량의 분포는 매우 다르며 우리는 우리가 사용하는 분포에 의존한 결론이 다를지 모른다는 것을 주목해야 한다.
그리고 어느 것도 분포가 정확하지 않다. Data 는 단지 다른 방법으로 조사한 것이다. 예를 들어, 만약 우리가 우주복을 만든다면 7000 의 큰 물체들을 피하기가 쉽고 모든 경우의 99.96%를 주의해야 한다고 말할지도 모른다. 그러나, 우주복에서 가장 중요한 것은 숫자에 의한 99.3%의 작은 입자에 대해 보호하는 것이다.
만약 우리가 위 표의 분포들의 평균을 계산한다면 수평균은 약 1.6cm 이고 질량 평균은 약 500cm 임을 알아야 할 것이다. - 그 만큼 매우 달라지는 것이다.
만약 전자현미경으로 입자를 측정한다면 앞의 내용(다른 기술은 다른 평균을 제공한다)으로 부터 D[1,0] 또는 수-길이평균 크기를 계산하고 있는 것을 알 수 있다. 만약 우리가 정말 요구하는 것이 질량 또는 부피의 평균 크기라면 수 평균을 질량 평균으로 바꿔야 한다. 수학적으로, 이것은 쉽게 실행 가능하지만, 우리는 이와 같은 변환의 결과를 측정해봐야 한다.
전기적 측정 기술이 평균 크기에서 오차가 ±3% 받는다고 생각해보자. 우리가 수 평균 크기를 질량평균 크기로 바꿀 때 질량평균은 직경의 입방체 함수로써 그때 오차는 마지막 값의 세제곱이 되거나 ±27% 가 될 것이다.
그러나 , 만약 레이저 확산으로 질량 또는 부피분포를 계산한다면 상황은 달라질 것이다. 용액분산법의 재순환 조건 하에 안정한 시료를 측정하는 경우 ±0.5%의 재사용 부피 평균을 발생시킬 수 있을 것이다. 만약 지금 이러한 부피평균을 수 평균으로 바꾼다면 오차 또는 수 평균은 0.5%의 세제곱근 이거나 1.0%보다 더 작을 것이다.
실제로 이것은 우리가 전자현미경을 사용하여 부피 또는 질량 분포를 원한다면, 10μ 한 개의 입자를 무시하거나 잃은 결과는 1μ 크기 천 개의 입자를 무시하거나 잃은 것과 같다는 것을 의미한다. 따라서 우리는 상호변환의 큰 위험성을 인식해야만 한다.
Malvern Sizers 에서 Dos 와 Windows 소프트웨어 둘 다 다른 지름을 구하는 것을 계산할 것이다. 그러나 우리는 이 지름들을 구할 때 매우 조심해야 한다. 다른 방법(의미)들은 다음에 나오는 식들(Hatch-Choate 변형 식-Ref.7) 에 의해 서로 다르게 변환 될 수 있다.
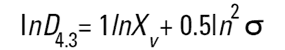
|
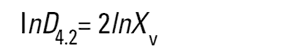
|
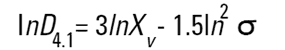
|
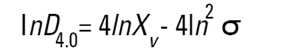
|
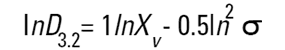
|
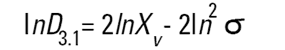
|
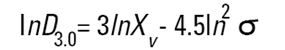
|
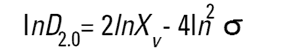
|
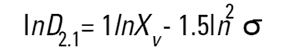
|
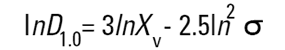
|
우리는 Malvern 레이저 회절 기술이 빛에너지 데이터 분석을 위한 부피 분포를 야기 시킨 다는 것을 보아 왔다. (Fraunhofer 분석에 의해 조사된 면적 분포가 가정되었다는 것에 주목한다.) 이 부피 분포는 위에 보여 진 것처럼 어떤 number 나 직경길이로 변환될 수 있다.
그러나, 어떤 분석 기술에서 우리는 이런 변환 된 결과(전 section 의 “number 와 길이 그리고 부피 / 질량 평균 간의 상호 전환”)를 알아야 하고, 또한 평균직경은 실제로 기계에 의해 측정되고, 어떤 직경은 실제로 계산되거나 첫 번째 측정된 직경에 의해 구해지는 것을 알아야 한다.
다른 기술들은 몇몇의 이미 측정된 직경들로부터 또 다른 직경들을 구할 수 있을 것이다. 예를 들어, 현미경은 D[1,0]을 측정 할 것이고 이것으로부터 다른 직경들을 구할 수 있을 것이다.
우리는 구해진 직경들 보다 측정된 직경들을 더욱 신뢰할 수 있다. 실제로 몇몇 실(제)예에서 구해진(계산된) 특성에 의존하는 것은 매우 위험할 수 있다. 예를 들어, Malvern 분석 표는 우리에게 특정 표면적(m2/cc 또는 m2/gm)을 제시한다. 우리는 표를 완전히 받아들이지 않아야한다. - 실제로, 만약 우리가 정말로 원하는 것이 물질의 특수한 표면적이라면 우리는 표면적을 계산 할 수 있는 특수한 기술인 B.E.T 또는 mercury porosimetry 를 사용해야 할 것이다.
이미 알고 있는 또 다른 기술은 입자의 다른 성질(혹은 크기)을 측정하고, 우리는 다른 평균 결과(D[4,3], D[3,2] 등)를 얻기 위한 많은 다른 방법 안에서 데이터를 사용해야 할 것이다. 그렇다면 우리는 왜 number 를 사용해야 할까? 1 과 10units 인 구의 지름들을 간단한 예로 알아보자. 우리가 금을 만들고 있다고 가정해보자. 만약 우리가 간단한 수 평균 직경을 계산한다면 이것은 다음과 같이 주어진다.
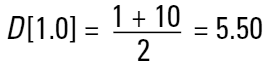
|
따라서 우리는 system 안에서 입자의 평균크기 는 5.50 units 라고 가정할 수 있을 것이다. 그러나 우리가 만약 우리가 금을 만들고 있다면 물질의 무게에 관심을 두어야 할 것이라는 것을 기억해야 한다.
예를 들어 만약 우리가 공정의 경향성을 알고 있다면 우리는 그곳에 350 만개의 입자가 들어 있다는 것에는 흥미가 없을 것이다.
그보다 우리는 1kg 이나 2kg 의 금이 있다는 것에 흥미를 둘 것이다.
질량평균이 직경의 입방체 함수라는 것을 기억하면 우리는 직경 1unit 인구는 1unit 의 질량을 가지는 것을 알 수 있고, 직경 10units 인구는 10=1000 units 의 질량을 가지는 것을 알 수 있을 것이다. 그것은 더 큰 구는 system 의 총 질량의 1000/1001 부분을 만든다는 것을 말한다. 만약 우리가 금을 만들고 있다면 우리는 1unit 인 구(sphere)는 던져 버릴 수 있을 것이다. 왜냐하면 우리는 system 총질량의 0.1% 보다 적게 잃을 것이기 때문이다.
따라서 수 평균은 시스템에서 도출된 질량에서 틀림없이 야기 될 것이다. 이것은 D[4.3]에서 좀 더 유용하다.
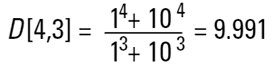
|
우리의 두 가지 구의 예시 속에서 질량이나 부피 평균 모멘트는 다음과 같은 식처럼 계산 되어 질 것이다.
이 수치는 우리에게 system 에서의 질량이 어디에 놓이는지 보여주고, 화학 공정 엔지니어에게는 가치 있는 수치가 된다. 그러나 우리가 clean room 안에서 실리콘이나 갈륨 arsenide wafers 를 만들고 있다고 가정해보자. 여기 만약 한 입자가 wafer 위에 놓여 진다면 defect 가 일어날 경향이 있다. 이러한 실제 예에서 보면 입자의 수나 농도가 매우 중요하다. 왜냐하면 1 개의 입자는 1 개의 defect 이기 때문에 우리는 직접적으로 입자들의 특정 개수나 입자들의 농도를 직접적으로 측정할 수 있는 기술을 사용하는 것을 원하게 된다. 본질적으로 이것은 입자 총수 와 입자 크기 간에는 다르다. 총 개수의 경우 우리는 각각의 입자를 기록하고 센다. 크기는 덜 중요하다. 그리고 우리는 오직 한계에 다다른 양의 크기의 스케일을 필요로 한다(8 에서 말함). 크기 적 관점에서 확실한 크기의 입자들은 크기나 입자들의 크기 기여도에 비해 관련이 적다.
그리고 우리들은 더욱 size bands 를 필요로 한다. 천식환자를 위한 1 회 분량의 인공호흡기를 측정해보면 약물의 농도와 입자 사이즈 기여도는 둘 다 중요하다.
이것들이 종종 통계학과 입자크기 분석에서 둘 다 잘못 사용되어 지기 때문에 이 3 가지 용어를 정의하는 것은 중요하다.
이것은 데이터의 어떤 산술평균이다. 입자들을 계산 할 수 있는 많은 평균이 있다. (section D[4,3]등을 참조)
이것은 정확히 모집단을 두 개로 동일하게 나누는 입자사이즈의 값이다. 예를 들면 위 값의 분포의 50%와 아래의 50%를 말한다.
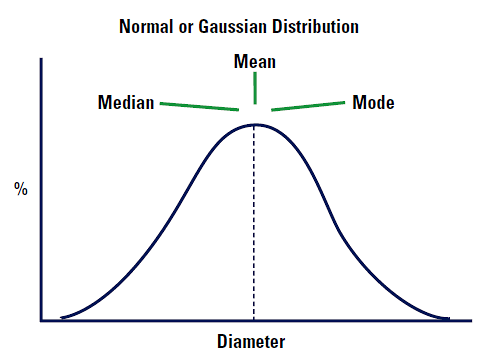
도수 곡선의 가장 높은 점과 같은 값은 도수 분포의 가장 흔한 값이다.
|
이 분포가 Nomal 혹은 Gaussian 분포라고 생각해보자. 평균, 중앙값, 최빈값은 정확히 같은 위치에 놓일 것이다. Fig 4 를 보아라.
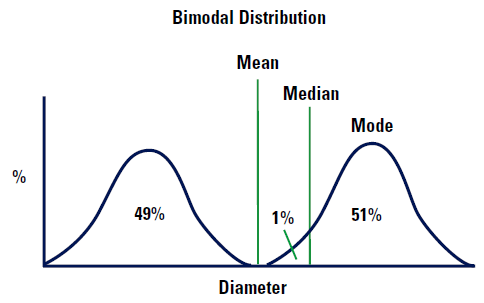
그러나 이 분포가 보기 5 와 같이 두 가지 모드(바이모달)라고 생각해보자.
|
평균 직경은 그래프에서 보이는 대로 거의 정확히 두 개의 분포 사이에 있을 것이다. 이런 평균 사이즈의 입자는 없다는 것을 유념해라. 중앙값 직경은 두 분포 중 높은 쪽으로 1%정도에 있을 것이다. 왜냐하면 이 포인트는 정확히 두 개의 분포로 나눌 것이기 때문이다. 최빈값은 더 높은 분포의 꼭지점일 것이다. 왜냐하면 이것은 직경의 가장 흔한 값이기 때문이다.
분포 대칭에 의해 좌우되는 평균, 중앙값, 최빈값이 이상적이거나 심지어 같아야 할 이유는 없다고 이 예시는 설명하고 있다.
Malvern 분포 테이블을 주목해라:
앞의 설명으로부터 입자의 다른 치수를 측정하기 때문에 우리는 각각의 측정 기술이 다른 결과를 생성해 낸다는 것을 볼 수 있었다. 우리는 이제 주된 다른 방법들에 대한 몇 가지 상대적 장단점을 토의할 것이다.
이것은 매우 오래된 기술이지만 저렴하고고 채굴에서 찾아진 큰 입자들에서는 쉽게 유용하다는 장점을 가지고 있다. Terence Allen 은 재생적인 sieving 의 어려움에 대해 논하지만 많은 사용자들의 주된 단점들은 다음과 같다.:
이것은 페인트와 세라믹 산업에서는 전통적인 방법으로 사용되어왔고, 매력적으로 낮은 답을 준다! 제조자가 요구할 것임에도 불구하고 적용 범위는 2~50 마이크론(Ref.1&2)이다.
측정의 원리는 Stokes' Law 방정식에 기초를 둔다.
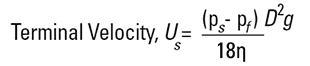
|
장비는 Andreason 피펫 만큼 단순할 수도 있고, 또는 원심분리기 또는 X-ray 의 사용을 포함해 더 복잡할 수도 있다.
이 방정식을 살펴보면 하나 또는 두 개의 잠재적 함정을 나타낼 것이다. 물질의 밀도는 필요하다. 따라서 이 방법은 물질이 자리잡지 않은 에멀젼 또는 밀도가 큰 물질이 빠르게 자리잡은 에멀젼에는 좋지 않다. 최종 결과는 Stokes 직경 (Dst)으로 이것은 무게 직경 D[4,3]과는 다르고, 간단히 같은 속도에서 구의 정착에 따른 입자 정착 속도의 비교다. 공통요소 안에서의 점도텀은 ‘1 도의 온도 변화가 2%의 점도를 변화시키도록 온도를 매우 정확하게 조절할 필요가 있다’는 것을 가리킨다.
방정식을 이용해 정착 시간을 계산하는 것은 비교적 쉽다. 이것을 한 개의 SiO2(밀도=2.5) 마이크론 입자는 20 도에서 물 속 중력 아래 1cm 로 굳어지는데 3.5 시간이 걸린다는 것을 보여준다. 그러므로 측정은 매우 느리고 지루한 측정을 반복하게 된다. 따라서 g 가 증가되게 움직이고, 상황을 치료하려고 시도한다
g 를 증가시키는 단점은 (Ref.3)에서 토의되었다. 침전 기술의 더 뚜렷한 비평들은 (Ref.2)에서 찾을 수 있다. 2).
Stoke's law 는 그들이 소유한 부피와 표면적이 가장 조밀한 모양이 되는 특이한 특징을 소유하는 구에서만 효과적이다. 따라서 더 불규칙적인 모양의 ‘보통’ 입자들은 구보다 더 넓은 표면적을 가질할 것이다. 그리고 이 입자들은 그들의 당량의 구형 직경들보다 증가된 방해성 때문에 더 느리게 떨어질 것이다.
| Displacement in 1.0 second (μm) | ||||||
|---|---|---|---|---|---|---|
| In air at 70°F (1atm) | In water at 70°F | In water at 70°F | ||||
| Particle diameter (µm) | Due to Brownian movement* | Due to Gravitational settling+ | Due to Brownian movement* | Due to Gravitational settling+ | Y | k=100Y(%) |
| 0.10 | 29.4 | 1.73 | 2.36 | 0.005 | 31.1 | (96.9) |
| 0.25 | 14.2 | 6.3 | 1.49 | 0.0346 | 3.15 | 75.9 |
| 0.50 | 8.92 | 19.9 | 1.052 | 0.1384 | 0.556 | 35.7 |
| 1.0 | 5.91 | 69.6 | 0.745 | 0.554 | 0.0983 | 5.0 |
| 2.5 | 3.58 | 400 | 0.334 | 13.84 | 0.00995 | 1.0 |
| 10.0 | 1.75 | 1550 | 0.236 | 55.4 | 0.00031 | 0.03 |
*Mean displacement given by equation (7.20)
+Distance settled by a sphere of density 2000kgm-3, including Cunningham's correction.
Y is defined in equation (7.23) (Taken from Reference 2 p 259)
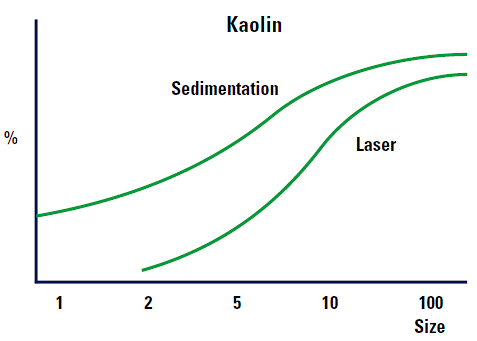
kaolin 과 같이 디스크 모양의 물질에서 이런 결과는 더 강조되고, 실제에서의 큰 굴곡들이 예상되어 진다.
게다가 작은 입자에서는 두 개의 경쟁적 힘(중력의 침적,Brownian 운동)이 있다. Stokes' law 는 중력의 침적에만 적용된다. 페이지 맨 위의 테이블은 두 경쟁적 힘 사이에서의 비교를 보여주고 있다. 만약 침적이 2μm 이하 크기의 입자에서 일어난다면 매우 큰 오차(대략 20%)들이 나올 것이라 보여진다. 그리고 오차들은 0.5μm 크기 입자들에서 과량의 100%이상 일어날 것이다.
침적 기술은 실제보다 더 작은 값을 나타내었고, 이것은 몇몇 제조업자들이 오해하고 있는 이유이기도 하다. 요약적으로 안료 사용자들을 위한 기술의 주된 문제점들은 아래와 같다:
보기 6 은 침적과 레이저 회절 결과 사이의 예상되는 차이를 보여주고 있다.
|
실제로 묽은 전해질 내에서 단일모드 현탁액으로 존재
하는 혈구를 배열하는데 있어서 이 기술은 1950 년대 중반에 개발되었다.
작동 원리는 매우 간단하다. 유리 용기는 구멍 또는 흠집을 그 안에 가지고 있다. 묽은 현탁액은 이 구멍으로 흘러 만들어지고, 전압은 그것을 가로질러 적용된다. 입자가 이 구멍을 통해 흐르기 때문에 전기용량은 바뀌게 되고, 이것은 전압 박동 또는 최고 피크에 의해 나타나진다. 기계 안에서 피크의 높이가 측정되고, 또 이것은 기준 latex 의 피크 높이와 관련이 있다 따라서 이 방법은 완전한 것이 아니지만 비교적 자연적인 방법이다. 광선 안의 입자 배향의 문제점들은 피크의 높이가 아닌 피크아래 면적을 측정함으로써 고쳐질 수 있다. 혈구들에 있어서 이 기술은 매우 뛰어나고, 이 방법은 개수를 세는 것과 부피분포 둘 다 구하는데 매우 유용하다. 실제로 안료(색소)와 같은 물질들을 다루는 산업에서는 기초적인 결점들이 많이 있다.:
그래서 요약적으로 이 기술은 혈구측정에는 매우 좋고, 많은 산업 물질에서의 애매한 성질들에 대해서는 좋지 않다.
궁금한 입자들을 직접적으로 볼 수 있기 때문에 microscopy 는 매우 뛰어난 기술이다. 입자의 모양을 볼 수 있고, 또 이것은 분산이 잘 되었는지 또는 시스템 내에 덩어리가 존재하는지를 판단하는데 사용되어진다. 이 방법은 비교적 싸고, 몇몇 현미경은 숫자들(보통 십진법의 6 또는 8 자리)을 얻어 이미지 분석을 하는데 사용된다.
10μm 크기(밀도 2.5)의 입자 1g 이 현미경으로도 각각 측정이 되지 않는 760*10^6 개의 입자들을 가지고 있다는 사실은 매우 흥미롭다.
그러나 위에서 언급된 형태의 간단한 판단 하에 특성 또는 생산이 기술을 조절하기 때문에 이것은 적합하지 않다. 상대적으로 측정되는 입자들은 거의 없고, 실제로 대표적이지 않은 샘플링의 위험성도 존재한다. 게다가, 무게 분포가 측정된다면 오차는 확대될 것이다. -10μm 크기의 입자 한 개를 잃거나 무시하는 것은 1μm 크기의 입자 1000 개를 무시하는 것과 같은 효과를 낸다.
전자 현미경은 샘플 표본을 정교하게 만들지만 속도가 느리다. 수동 현미경의 경우, 측정되는 입자들이 거의 없고(훌륭한 오퍼레이터는 하루에 2000 개 측정), 오퍼레이터들이 빠르게 지친다. “어느 디멘전을 측정할 것인가?”의 문제가 있다. 따라서 같은 샘플에 대해 오퍼레이터의 판단이 크게 작용한다. 회절과 같이 측정할 경우, 현미경은 입자들을 특징 짓는데 매우 유용한 도움을 준다
이것을 좀 더 정확하게 부르면 low angle laser light scattering(LALLS)라고 할 수 있다. 이 방법은 특성과 품질을 조절하는데 있어서 많은 산업에 선호된 방법이다. ISO13320 에 따르면 가장 적정한 범위는 0.1~3000 마이크로미터 이다. 산업은 최근 20 년 동안 이러한 범위를 넘어서 발전해왔다. 방법은 회절각이 분자 사이즈에 반비례 한다는 사실에 기초해 믿어져 왔다. 기기에 의한 결론은 :
오래된 기기와 현존 하는 몇몇 기기들은 대략적인 Fraunhofer 가정에 의해 신뢰할 수 있는데
이러한 가정은 많은 물질과 작은 물질에 대해 절대 맞지 않고 에러율이 30%에 이르고 물질의 굴절률과 관계 있고 중간 특성과도 관계가 있다. 입자의 사이즈가 스캐터링 파장에 접근하면 최대와 최소 함수 관계로 복잡해진다. 최근의 기기들(Mastersizer 2000 에 이르는 Malvern 기기와 같은)은 빛과 물질간의 복잡한 상호작용 식을 풀기 위해 Mie 이론을 모두 사용한다. 이것들은 큰 사이즈 범위에서도 정확한 값들을 측정할 수 있다(0.02- 2000 마이크로미터까지). Mie 이론은 투영된 면적을 측정하는 Fraunhofer 와는 반대로 입자의 부피를 측정한다.
이런 완전한 정확도의 “단점”은 물질과 매질의 굴절률을 알아야 한다는 것이고 굴절되는 빛이 흡수하는 부분의 굴절률을 알고 있거나 추측할 수 있어야 한다는 것이다. 그러나 다수 사용하는 사람들은 이러한 수치들이 이미 알려져 있거나 측정이 가능하기 때문에 문제가 되지 않는다.
레이저 회절은 다음의 장점들을 가지고 있다.:
1. Paint and Surface coatings - theory and practice; Ed. R. Lambourne Ellis Horwood Ltd. 1993. ISBN 0-13-030974-5PGk
2. Particle Size Measurement;T. Allen, Chapman & Hall. 4th Edition, 1992. ISBN 04123570
3. G.J.J.Beckers, H.J.Veringa; Powder Technology 60 (1989) p245-248.
4. J. Ranucci Pharmaceutical Technology; October 1992 pp 108-114.
5. G. Hind; Manufacturing Chemist August 1990 pp 28-30.
6. M.W.Wedd; ILASS-Europe 8th Annual conference, Koninklijke/Shell Laboratorium, Amsterdam 30 September -2nd October, 1992.
7. T. Hatch & S.P Choate. J. Franklin Inst. 207 pp 369-387 (1929).