La diffusion statique de la lumière est une technique permettant de mesurer la masse molaire à l'aide du rapport entre l'intensité de la lumière diffusée par une molécule et ses valeurs de masse molaire et de taille moléculaire. Ces relations sont décrites par la théorie de Rayleigh, selon laquelle la masse molaire d'une molécule est proportionnelle au rapport de Rayleigh de lumière diffusée, c'est-à-dire le rapport de l'intensité de lumière diffusée sur l'intensité de lumière incidente.
Tous les instruments de diffusion statique de la lumière détectent la quantité de lumière diffusée par un échantillon afin de mesurer sa masse molaire. Cependant, dans la mesure où les molécules grandissent, un deuxième facteur, la dépendance angulaire, entre en ligne de compte. La dépendance angulaire affecte l'intensité de la lumière diffusée et, par conséquent de la masse molaire calculée. Il est donc nécessaire de la prendre en considération.
| GPC | Chromatographie par perméation de gel |
| SEC | Chromatographie d'exclusion stérique |
| LALS | Diffusion de la lumière à petit angle |
| RALS | Diffusion de la lumière à angle droit (diffusion de la lumière à 90°) |
| MALS | Diffusion de la lumière multi-angle |
| SLS | Diffusion statique de la lumière |
| DLS | Diffusion dynamique de la lumière |
| Rg | Rayon de giration |
| RH | Rayon hydrodynamique |
| MW | Masse molaire |
| Mn | Masse molaire moyenne en nombre |
| Mw | Masse molaire moyenne en poids |
| Mz | Z-Average de masse |
| A2 | Second coefficient de Viriel (B22) |
La diffusion de la lumière est un domaine qui peut prêter à confusion. De nombreuses techniques relèvent du domaine général de la diffusion de la lumière, qui permet de mesurer un éventail de paramètres. Les frontières entre ces catégories sont parfois floues, car certains systèmes emploient plus d'une technique dans le même instrument. Il est donc facile de perdre de vue les facteurs les plus importants en recherchant la technologie de diffusion de la lumière la plus adaptée à votre application.
La diffusion statique de la lumière, que l'on appelle également diffusion classique de la lumière, est une technique permettant de mesurer la masse molaire et le rayon de giration moléculaire. Dans le secteur de la diffusion statique de la lumière, figurent diverses technologies désignées par des acronymes tels que SLS, MALS, LALS et RALS. Chacune possède des différences subtiles et présente ses propres avantages et inconvénients.
Le présent livre blanc décrit en détail les principes et théories qui sous-tendent la diffusion statique de la lumière. Nous décrirons et comparerons la théorie, la technique et les différentes technologies mises en œuvre. Ce livre blanc vous aidera à saisir les fondamentaux de ces mesures et à choisir de manière judicieuse la solution la plus adaptée à votre application.
Vous trouverez dans chaque section des explications détaillées. Chaque section propose en préambule une synthèse de son contenu décliné en quelques points clés, pour vous aider à décider si sa lecture est pertinente.
La masse molaire est une propriété qui décrit la masse d'une molécule individuelle. Scientifiquement, il s'agit de la masse d'un matériau requise pour générer 1 mole de l'échantillon. Par exemple, le carbone a une masse molaire de 12 g/mol. Les unités de masse molaire s'expriment en grammes par mole (g/mol). Cependant, elles sont parfois exprimées en daltons (Da), voire en kilo-daltons (kDa), ce qui s'avère plus pratique.
On considère qu'un échantillon de protéines pures affiche une masse molaire fixe et que toutes les molécules de protéines au sein de l'échantillon ont une masse molaire égale. Pour un échantillon de polymère naturel ou synthétique, la distribution de la masse molaire des molécules dans un échantillon particulier peut être très variable. Le terme « polydispersité » désigne l'étendue de la gamme de distribution. On dit d'un échantillon avec une gamme très étroite de masses molaires qu'il a une polydispersité faible ou qu'il est très monodispersé. On dit d'un échantillon avec un plus large éventail de masses molaires qu'il a une polydispersité élevée.
La majorité des échantillons contiennent une gamme de masses molaires, notamment les polymères naturels et synthétiques. Il existe plusieurs manières de décrire la distribution de la masse molaire. L'une des méthodes les plus courantes consiste à utiliser les moments de masse molaire Mn, Mw et Mz, respectivement les masses molaires moyennes en nombre, en poids et en z-Average. Ces valeurs sont définies par les équations présentées ci-dessous, dans lesquelles ci et Mi correspondent à la concentration et à la masse molaire pour chaque tranche de données :

|

|

|
On peut intuitivement déduire que la masse molaire moyenne en nombre correspond à la masse totale de matière, divisée par le nombre total de molécules et qu'il s'agit donc d'une moyenne numérique. Cette méthode privilégie les molécules de masse inférieure, qui sont plus nombreuses. Diverses propriétés telles que la baisse de la pression de la vapeur, l'abaissement cryoscopique et la pression osmotique dépendent du nombre de molécules, et non pas de leur taille. Le calcul de la masse molaire moyenne en poids s'effectue en multipliant la masse des molécules, de sorte que la moyenne privilégie les molécules plus grosses dans la distribution. Les propriétés telles que la diffusion, la sédimentation et la diffusion de la lumière dépendent à la fois de la taille et de la masse des molécules. La moyenne z (z-Average) de masse molaire implique une autre multiplication de la masse molaire des molécules. Elle privilégie donc nettement les plus grosses molécules de l'échantillon. Il est possible de la déterminer directement à l'aide de la technique de l'ultracentrifugation.
En utilisant ces trois valeurs, il est possible d'obtenir une idée de l'ensemble de la distribution de masses molaires. Bien sûr, plus ces valeurs sont proches les unes des autres, plus la polydispersité est basse, et plus elles sont éloignées les unes des autres, plus la polydispersité est élevée. La polydispersité se définit selon l'équation
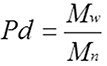
|
Puisque la valeur Mw est toujours supérieure ou égale à Mn, la valeur la plus basse possible pour la polydispersité (Pd) est 1, mais il n'y a pas de limite supérieure théorique. Les polymères naturels et synthétiques ont un large éventail de polydispersités, mais puisque les protéines ont des masses molaires fixes, nous pouvons nous attendre à une polydispersité de protéine très faible (proche de 1) pour les protéines qui se comportent correctement.
La taille moléculaire correspond à la taille physique d'une molécule. Habituellement, une valeur unique permet de décrire la taille. Cette valeur correspond au rayon d'une sphère d'une taille équivalente à la molécule mesurée. Les deux valeurs de taille moléculaire les plus couramment utilisées sont RH (rayon hydrodynamique) et Rg (rayon de giration). Le rayon hydrodynamique correspond au rayon d'une sphère équivalente, affichant une vitesse de diffusion égale à celle de la molécule étudiée. Il est calculé à partir de la diffusion dynamique de la lumière ou de la viscosité intrinsèque, et ne sera donc pas pris en considération ici. (Pour de plus amples informations sur le rayon hydrodynamique, nous vous invitons à consulter les notes techniques « Dynamic Light Scattering: An Introduction in 30 Minutes » (Diffusion dynamique de la lumière : Présentation en 30 minutes) et « Protein and polymer molecular size by GPC/SEC » (Détermination des tailles moléculaires des protéines et des polymères par GPC/SEC), disponibles sur le site Web de Malvern).
Le rayon de giration correspond à la valeur quadrique moyenne des rayons allant du centre de masse aux différents cœurs de masse au sein de la molécule. On désigne parfois cette valeur sous l'appellation Rrms (root-mean-square en anglais). L'unité de taille moléculaire est le nanomètre (nm). Rg se calcule à l'aide d'une diffusion statique de la lumière. Nous allons étudier cette valeur en détail dans la suite du document.
Quand un photon percute une molécule, une partie de l'énergie du photon sert à amorcer un phénomène dit de dipôle oscillant au sein de la molécule. Cette énergie est ensuite renvoyée par la molécule dans toutes les directions sous forme de lumière. Nous pouvons voir ce phénomène dans la vie de tous les jours, en observant des nuages blancs, des couchers de soleil ou de la poussière passant dans un rayon de soleil ou dans le faisceau lumineux d'un projecteur. Les principes qui sous-tendent la diffusion de la lumière peuvent être exploités pour mesurer un certain nombre de propriétés liées à la molécule.
Les propriétés de la lumière diffusée par les molécules et les particules varient selon l'objet réalisant la diffusion, tel que défini dans l'équation de Rayleigh.

|
où :

|
où :

|
où :
En termes plus simples, l'équation de Rayleigh nous indique que l'intensité de la lumière diffusée à un angle donné dépend d'un certain nombre de facteurs, notamment la masse molaire et la taille moléculaire de l'échantillon étudié. Comme le montre l'équation de Rayleigh, les molécules avec des masses molaires supérieures et de grandes tailles dispersent davantage la lumière. Alors que l'augmentation de l'intensité de la lumière diffusée est linéaire par rapport à la masse molaire, elle n'est pas linéaire par rapport à la taille.
Donc, si nous connaissons tous les autres facteurs dans l'équation de Rayleigh, nous pouvons mesurer l'intensité de la lumière diffusée (par rapport à Rθ) et calculer la masse molaire de l'échantillon.
La diffusion statique de la lumière (SLS) emploie une configuration optique permettant de rendre le signal détecté « statique » ou stable. En mesurant l'intensité de la lumière diffusée par un échantillon dans des situations où les autres constantes sont connues, la masse molaire de l'échantillon peut être calculée.
Le terme « diffusion statique de la lumière » est utilisé pour différencier cette technique de la diffusion dynamique de la lumière, une technique différente mais voisine, servant à mesurer la taille des particules. Pour obtenir plus d'informations sur la diffusion dynamique de la lumière, voir la note technique de Malvern « Dynamic Light Scattering: An Introduction in 30 Minutes » (Diffusion dynamique de la lumière : Présentation en 30 minutes) ou le livre blanc « A basic guide to particle characterization » (Un guide de base sur la caractérisation des particules) sur le site Web de Malvern.
Des mesures de diffusion statique de la lumière peuvent être effectuées en cuvette ou avec la technique de chromatographie par perméation de gel (GPC)/chromatographie d'exclusion stérique (SEC). L'utilisation d'un système de chromatographie supprime un certain nombre de problèmes associés à la préparation et purification de l'échantillon, ce qui fait de cette méthode de mesures SLS l'une des plus fréquentes. En outre, la GPC/SEC nous permet de combiner facilement les données de diffusion de la lumière avec des données provenant d'un détecteur de concentration pour mesurer la concentration de l'échantillon au même moment, et donc utiliser ces deux groupes de données dans nos calculs. Le détecteur de concentration le plus courant est le réfractomètre (RI), mais il également possible d'avoir recours à un détecteur d'absorbance d'ultraviolet (UV).

|
L'équation de Rayleigh présentée ci-dessus comprend le terme 1/Pθ, dont jusqu'à présent nous avons supposé connaître les valeurs. Toutefois, ce n'est pas vrai, et c'est ici que toutes les différences entre les différents instruments de diffusion de lumière entrent en jeu.
La valeur Pθ, ou facteur de forme, dépend de la taille de la molécule et de l'angle de diffusion déterminé. Ce terme est défini comme :

|
où :
L'équation indique que 1/Pθ est tributaire d'un certain nombre de facteurs liés à l'échantillon et la mesure. Ceux-ci comprennent l'indice de réfraction du solvant (n0), la longueur d'onde laser dans une chambre vide (λo), l'angle de mesure (θ) et la taille de la molécule mesurée Rg).
Cela signifie que pour les plus grosses molécules, la quantité de lumière diffusée dépend de l'angle de mesure. Ce phénomène de « dépendance angulaire » s'explique par le fait qu'à mesure que la taille moléculaire augmente, les photons ne sont plus dispersés indépendamment, mais produisent des interférences mutuelles constructives et destructives, comme l'illustre la Figure 2.

|
Lorsque la molécule est petite par rapport au laser, comme dans la Figure 2A, son action s'apparente à celle d'un diffuseur ponctuel. Dans cette situation, la lumière est dispersée par la molécule avec une intensité égale dans toutes les directions. Ces molécules sont appelées « diffuseurs isotropes ».
Toutefois, à mesure que la molécule grossit par rapport au laser, la taille et la structure de la molécule commencent à jouer un rôle important. Les photons individuels du laser sont diffusés par différents points à l'intérieur de la molécule. Ce phénomène est dépendant de Rg. Ces photons dispersés présentent des variations de phase, ce qui provoque des interférences mutuelles. L'intensité mesurée résultante dépendra du poste d'observation. Ces molécules sont appelées « diffuseurs anisotropes ». Aux tailles qui nous intéressent, toute l'interférence est destructive, ce qui signifie que l'intensité semblera toujours plus basse que si nous avions supposé qu'il s'agissait d'un diffuseur isotrope. Si nous utilisions cette intensité pour calculer la masse molaire à l'aide de l'équation de Rayleigh, nous intègrerions donc une sous-estimation.
Afin d'éliminer cet effet, l'équation de Rayleigh nous dit que si nous devions mesurer l'intensité de la lumière diffusée à un θ de 0°, alors sin2(θ/2) aurait une valeur de 0 et 1/Pθ une valeur de 1. Ainsi, à 0°, l'intensité de la lumière diffusée ne serait pas affectée par l'interférence et nous pourrions établir un lien entre l'intensité et la masse molaire, comme avec les molécules plus petites, lors de mesures à un angle de 90°. Il est malheureusement impossible d'atteindre ces conditions, car l'intensité du laser d'illumination à 0° est nettement supérieure à la lumière diffusée, ce qui empêche de séparer la lumière purement dispersée. Il est impossible d'effectuer des mesures directes à 0°, ce qui nous contraint à employer une autre méthode.
La règle empirique à utiliser pour déterminer le point de départ de la dépendance angulaire consiste à considérer qu'à un diamètre inférieur à 1/20ème de la longueur d'onde laser, une diffusion isotrope des molécules se produit et qu'au-delà, il s'agit d'une diffusion anisotrope. La plupart des instruments sont dotés de lasers dont les longueurs d'onde sont comprises entre 633 et 670 nm (rouge). Ainsi, la limite de la diffusion isotrope est comprise entre 15,8 et 16,8 nm de rayon (en raison de la dépendance envers la longueur d'onde laser, le même calcul pour un laser d'une longueur d'onde de 532 nm (vert) permet d'obtenir une valeur de 13 nm).
Cette valeur nominale approximative d'un rayon de 15 nm pour le point de départ d'une dépendance angulaire mesurable sera également le seuil inférieur auquel il est encore possible de mesurer la taille moléculaire, Rg. (Voir « Comment obtenons-nous la taille moléculaire, Rg, à partir des données ? », ci-dessous)
Les différents types d'instruments de mesure de la diffusion de la lumière sont conçus pour surmonter les problèmes de dépendance angulaire de différentes manières, que nous allons aborder dans la section suivante.
Afin de remédier à la dépendance angulaire, nous devons décider quelle est l'intensité de la lumière diffusée à 0° en fonction des données obtenues avec d'autres angles. La meilleure façon de calculer et d'illustrer ce phénomène est d'utiliser un « tracé de Guinnier », version simplifiée d'un tracé de Zimm dans lequel le second coefficient de Viriel n'est pas nécessaire.
Un tracé de Guinnier est un tracé de KC/Rθ en fonction de l'angle (sin2(θ/2)). D'autres tracés et modèles sont disponibles, mais celui-ci est le plus commun. Un exemple est illustré à la figure 3.

|
Les mesures de l'intensité de la diffusion de la lumière sont effectuées à l'angle désiré. En connaissant la concentration et d'autres facteurs concernant l'échantillon,
Il est possible de calculer KC/Rθ et de le représenter dans le graphique sous forme de fonction de sin2 (θ/2). L'ordonnée à l'origine (équivalant à un angle de 0°) est de 1/Mw, d'où la masse molaire peut être aisément calculée.
La pente initiale de la ligne est :

|
Rg peut ensuite être calculé à partir de cette équation avec une relative facilité. Toutefois, à de petites tailles moléculaires, la pente sera très faible et cachée dans le bruit des données. C'est uniquement lorsque la molécule est d'une taille appréciable par rapport à la longueur d'onde de la lumière laser que la pente sera suffisamment prononcée pour obtenir une valeur de Rg fiable. Comme nous l'avons expliqué ci-dessus, le seuil nominal d'un laser de 633 nm est une valeur Rg ≈15 nm. Cependant, la limite absolue dans le cadre de la mesure de Rg peut être supérieure ou inférieure au seuil nominal de 15 nm, selon l'échantillon, le solvant et les conditions de mesure. De nombreux fabricants d'instruments de type MALS assortissent les caractéristiques techniques de leurs produits d'une limite de 10 nm (voire encore plus basse). Cela concerne souvent les polymères normaux, présentant des valeurs dn/dc élevées et de fortes concentrations, dans des conditions idéales. En pratique, il s'avère impossible d'obtenir cette limite sur tous les échantillons. Pour ce qui est de l'autre extrémité des valeurs, avec des échantillons présentant des valeurs dn/dc run médiocres dans des conditions non idéales, la plus petite valeur Rg pouvant être mesurée pourrait être nettement supérieure au seuil nominal de 15 nm.
Il existe quatre types d'instruments SLS. RALS, LALS, systèmes hybride RALS/LALS et MALS.
Un appareil RALS est le plus simple de tous les instruments de diffusion de la lumière. Il mesure l'intensité de la lumière dispersée à 90° par rapport au faisceau incident, comme l'illustre la Figure 4A. La masse molaire de l'échantillon est ensuite calculée directement à partir de l'intensité mesurée et de la concentration de l'échantillon. Dans le tracé Zimm de la Figure 4B, l'intensité de la lumière diffusée est mesurée loin de l'axe y et on suppose que la dispersion de l'échantillon est isotrope (c'est-à-dire égale à tous les angles).

|
Un système RALS présente divers avantages :
Cependant, les détecteurs RALS présentent certaines limites :
Sachant que la taille des protéines est presque toujours inférieure au rayon de 15 nm et qu'elles ne permettent qu'une diffusion faible de la lumière, elles nécessitent un détecteur sensible. Les détecteurs RALS excellent donc dans la mesure de la masse molaire des protéines.
Un détecteur LALS mesure l'intensité de la lumière diffusée à un angle aussi proche que possible de 0°, comme l'illustre la Figure 5A. Cette méthode présente l'avantage de mettre en œuvre une intensité très proche de sa valeur à 0°. Ainsi, la masse molaire calculée sera très proche de la masse molaire réelle de la molécule. Pour être considéré comme un détecteur LALS, son angle doit être inférieur à 10° et les détecteurs LALS les plus courants présentent un angle de mesure de 7°. Cependant, plus l'angle de mesure approche de 0°, plus la mesure sera précise, et ce, quelle que soit la taille de la molécule mesurée. En observant le tracé de Zimm (Figure 5B), une mesure LALS est très proche de l'axe et donc très proche de l'ordonnée à l'origine. Cela signifie que lors d'une mesure à 7°, l'erreur est très basse. Avec une mesure LALS à 7°, sin2(θ/2) est de seulement 0,0037, ce qui correspond à moins d'1 % d'erreur pour la masse molaire, même chez les plus grosses molécules.

|
Un système LALS présente divers avantages :
Les détecteurs LALS présentent également certaines limites :
Globalement, les mesures LALS permettent une mesure précise de la masse molaire à l'aide d'une diffusion statique de la lumière. Les systèmes LALS sont particulièrement utiles pour mesurer la masse molaire de gros diffuseurs anisotropes, tels que les polymères synthétiques et naturels.
Les éléments abordés ci-dessus attestent de la complémentarité des détecteurs RALS et LALS. Les détecteurs RALS sont assez sensibles pour mesurer de petits diffuseurs isotropes, tandis que les détecteurs LALS peuvent mesurer la masse molaire de grosses molécules à un degré de précision sans équivalent. Un modèle hybride RALS/LALS permet donc d'associer ces deux mesures au sein d'une cellule unique, comme l'illustre la Figure 6A. Sur le tracé de Zimm, le détecteur RALS permet de mesurer les molécules d'une taille inférieure au seuil de diffusion isotrope de ≈15 nm. Le détecteur LALS permet de mesurer avec précision les molécules d'une taille supérieure au seuil de diffusion isotrope de ≈15 nm. Le logiciel sélectionne automatiquement la configuration LALS ou RALS selon les signaux reçus par le détecteur. Pour les échantillons assurant une diffusion anisotrope, le rapport des deux masses molaires calculées peut servir à obtenir une estimation de Pθ. Cela permet ensuite d'estimer la valeur Rg, en supposant un modèle structurel, tel qu'une pelote aléatoire ou une sphère rigide.

|
L'association RALS/LALS permet de bénéficier des avantages des deux systèmes :
Le système hybride RALS/LALS présente les limites suivantes :
Dans l'ensemble, un système hybride RALS/LALS présente les avantages des systèmes RALS et LALS sans pâtir de leurs inconvénients. Grâce à ces propriétés, le système hybride RALS/LALS excelle dans la mesure de la masse molaire de tout échantillon.
Comme leur nom l'indique, les détecteurs MALS mesurent l'intensité de la lumière diffusée à de multiples angles, comme l'illustre la figure 7A. En reliant ces points sur un tracé de Zimm (figure 7B), on peut extrapoler une ligne droite illustrant la trajectoire optimale jusqu'à 0°, afin de calculer la masse molaire. La pente initiale de cette ligne permet un calcul précis de la taille moléculaire, Rg.

|
Les détecteurs MALS présentent un certain nombre d'avantages spécifiques :
Toutefois, les systèmes MALS présentent également des limites :
Lorsque vous effectuez des mesures à l'aide d'un système MALS, le facteur le plus important réside dans le fait que la forme de l'extrapolation est inconnue. L'ajustement dépend en grande partie du nombre d'angles bas et de la précision des points. Il est donc important qu'un instrument MALS présente autant d'angles faibles que possible, car cela fournira l'extrapolation la plus exacte à 0°. En règle générale, pour optimiser la précision de l'extrapolation, il est utile de pouvoir utiliser un plus grand nombre d'angles.
Pour résumer, le système MALS constitue une solution universelle permettant de mesurer la masse molaire et la valeur Rg de tous les types d'échantillons, mais la nature de sa conception impose certains compromis en matière de mesure.
Les techniques de diffusion de la lumière sont souvent désignées comme « absolues », mais cette notion n'est pas bien comprise.
Bien que la colonne n'ait pas véritablement besoin de calibration, tous les appareils de diffusion de la lumière nécessitent une forme d'étalonnage. La seule question concerne le mode de calibration de l'appareil, qui peut s'effectuer de différentes manières :
Le principe de calibration de la dispersion de la lumière, à l'instar de toutes les calibrations, consiste à faire correspondre la taille du signal au paramètre mesuré. En matière de diffusion statique de la lumière, il s'agit de corréler l'amplitude du signal à partir du photo-détecteur à l'intensité de la lumière diffusée, puis à la masse molaire de l'échantillon. Outre les facteurs dépendants de l'échantillon décrits dans l'équation de Rayleigh, l'intensité mesurée de la lumière diffusée dépendra d'un grand nombre de variables dépendantes de l'instrument, notamment :
Il est impossible de caractériser l'ensemble de ces éléments dans un système en employant un degré de précision requis pour la mesure. Ils sont donc tous pris en considération dans une étape de calibration.
Il existe deux méthodes permettant de calibrer un système, mais elles sont identiques sur le plan pratique.
Le principe sous-tendant une calibration de masse molaire basée sur un standard est de passer un échantillon de masse molaire connue à travers le détecteur SLS pendant qu'il est connecté à un système GPC/SEC. L'amplitude du signal du détecteur de diffusion de la lumière et la concentration connue de l'échantillon, la masse molaire et le dn/dc sont utilisés pour calculer un facteur de réponse de l'instrument ou de constante de calibration pour le détecteur de dispersion de la lumière. Sans tenir compte d'autres valeurs telles que l'indice de réfraction du solvant et la longueur d'onde du laser, la calibration du détecteur de diffusion de lumière constante est définie comme :

|
où :
Avec un standard, la concentration et le volume d'injection (et donc la masse) sont connus, car il s'agit de la masse molaire et du dn/dc standard.
Ceci permet de calculer la constante de calibration et peut être réalisé simultanément sur chaque angle dans un détecteur de diffusion de la lumière.
Une fois la constante de calibration déterminée, la masse molaire de n'importe quel échantillon peut être mesurée :

|
où :
Mw = masse molaire de l'échantillon,
δLS = intensité de lumière diffusée mesurée par l'échantillon,
dn/dc = incrément d'indice de réfraction de l'échantillon,
mass = masse injectée de l'échantillon.
kls = la constante de calibration de la diffusion de la lumière,
Dans un système GPC/SEC contenant plusieurs détecteurs, chacun d'eux peut être calibré en même temps à l'aide d'un standard bien caractérisé et traçable. Autre avantage de la calibration des détecteurs de cette façon : les volumes inter-détecteur entre les différentes cellules du détecteur et l'élargissement de la bande qui se produit lorsque l'échantillon passe entre des détecteurs peuvent être quantifiés dans une même étape.
L'avantage final de cette méthode est que la calibration du système peut être contrôlée et/ou ré-étalonnée à tout moment par l'utilisateur. Cet aspect est particulièrement utile, car les constantes de l'instrument dérivent au fil du temps en raison d'un certain nombre de facteurs tels que la détérioration des sources de lumière, la propreté des cellules, le changement de tubes du détecteur et autres.
Une calibration de masse molaire basée sur un standard permet donc de calculer tous les facteurs de réponse de l'instrument et les constantes de calibration simultanément au calcul des volumes inter-détecteur et paramètres d'élargissement du pic. Il offre le moyen le plus efficace de calibration d'un système et de par sa nature même, il constitue également un moyen de vérifier la calibration d'un système en comparant les réponses du standard au moment de la calibration.
Le principe qui sous-tend une calibration par diffusion basée sur standard consiste à remplir la cellule de mesure de la diffusion de lumière en utilisant un solvant dont on connaît les propriétés de diffusion de la lumière, tel que du toluène. Le toluène présente un rapport de Rayleigh bien caractérisé (rapport de l'intensité de lumière diffusée sur l'intensité de lumière incidente). Ainsi, en mesurant le signal de diffusion observé à partir du toluène, on peut calculer le signal de diffusion de l'échantillon. Rθ pour l'échantillon se calcule selon l'équation suivante :
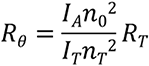
|
où :
La masse molaire de l'échantillon est ensuite calculée en intégrant cette valeur Rθ à l'équation de Rayleigh. Cela signifie que la constante de calibration dans cette situation est essentiellement :

|
Bien qu'il ne soit pas nécessaire de disposer d'une valeur de masse molaire pour calibrer un détecteur, le principe de calibration avec un standard de diffusion est identique, puisqu'on utilise un standard pour mesurer la réponse du détecteur de diffusion de lumière vers un échantillon connu.
Cette méthode présente plusieurs inconvénients majeurs :
Dans l'ensemble, une calibration par diffusion basée sur standard constitue une méthode plus laborieuse qui n'améliore pas la calibration et ne fait qu'ajouter des obstacles à la calibration correcte d'un système.