Cette question peut sembler assez évidente. Cependant, elle revêt un caractère essentiel à la compréhension des résultats provenant de diverses techniques d'analyse de la taille des particules. Les processus de dispersion et la forme des matériaux font de l'analyse de la taille des particules un sujet bien plus complexe qu'il n'y paraît.
Imaginez que je vous demande de mesurer une boîte d'allumettes avec une règle. Vous pourriez répondre que la boîte d'allumettes mesure 20 x 10 x 5 mm. Il serait inexact de dire que la boîte d'allumettes mesure 20 mm, car cela ne fait référence qu'à une de ses dimensions. Il est donc impossible de catégoriser une boîte d'allumettes en trois dimensions à l'aide d'un seul nombre..
Évidemment, cette situation est encore plus compliquée pour des formes complexes, telles qu'un grain de sable ou un pigment de peinture. Les responsables de l'assurance qualité ne veulent utiliser qu'un seul chiffre pour décrire leurs particules. Ils cherchent à savoir si la taille moyenne d'un produit a augmenté ou diminué par rapport au lot précédent. C'est là que réside le problème principal dans l'analyse de la taille des particules : comment décrire un objectif tridimensionnel à l'aide d'un seul nombre ?

|
Il n'existe qu'une seule forme pouvant être décrite par un nombre unique : la sphère. Quand on dit qu'une sphère mesure 50 μ, cela constitue une description parfaite. Ce n'est pas le cas même pour un cube, car la valeur de 50 μ pourrait désigner un côté ou une diagonale. En ce qui concerne notre boîte d'allumettes, diverses propriétés peuvent être représentées par un nombre unique. Par exemple, sa masse s'exprime par un chiffre, tout comme son volume et sa surface. Ainsi, en disposant d'une technique permettant de mesurer la masse de la boîte d'allumettes, nous pouvons convertir cette masse en masse d'une sphère, en nous rappelant que...
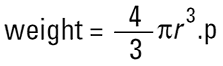
|
et calculer un nombre unique (2r) pour le diamètre de la sphère d'une masse équivalente à celle de notre boîte d'allumettes. Il s'agit de la théorie de la sphère équivalente. Nous mesurons une propriété de notre particule et supposons que cette valeur fait référence à une sphère, ce qui nous permet d'obtenir un nombre unique (le diamètre de cette sphère) pour décrire la particule. Ainsi, il n'est pas nécessaire de décrire des particules en 3D à l'aide d'au moins trois nombres. En effet, bien que cette abondance de chiffres permette de gagner en précision, elle n'est pas facile à utiliser sur le plan pratique.
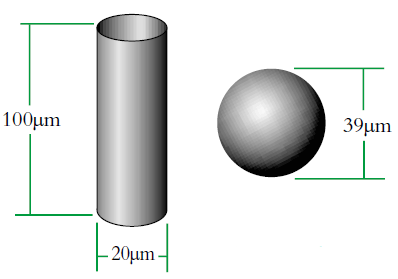
Nous pouvons observer que cette approche produit des effets intéressants selon la forme de l'objet, comme l'illustre l'exemple des sphères équivalentes des cylindres (Fig. 2). Cependant, tout changement de la forme ou du poids du cylindre entraînera un changement de volume/ masse, ce qui nous permettra de déduire notamment une augmentation ou une réduction de la taille, grâce au modèle de la sphère équivalente.
|
Imaginons un cylindre de diamètre D1 = 20 μm (donc, r=10 μm) et d'une hauteur de 100 μm.
Il existe une sphère de diamètre D2 dont le volume est équivalent au cylindre. Nous pouvons calculer ce diamètre de la manière suivante :
Volume du cylindre =
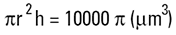
|
Volume de la sphère =
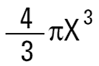
|
Où X correspond au rayon de volume équivalent.
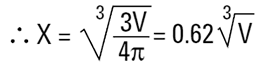
|
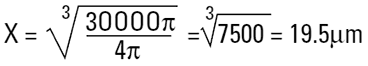
|
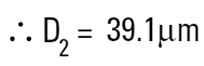
|
Le diamètre de la sphère équivalente en volume, pour un cylindre de 100 μm de hauteur et 20 μm de diamètre, est d'environ 40 μm. Le tableau ci-dessous indique les diamètres sphériques équivalents pour des cylindres de divers rapports géométriques. La dernière ligne peut illustrer une grande particule d'argile aux formes irrégulières. Elle semble mesurer 20 μm de diamètre, mais comme elle ne fait que 0,2 μm d'épaisseur, nous ne prenons normalement pas en compte cette dimension. Un instrument mesurant le volume de la particule nous donnerait une valeur approximative de 5 μm. C'est pourquoi il est légitime de remettre en question les réponses obtenues selon différentes méthodes !
Remarquez également que tous ces cylindres sembleront avoir la même taille pour un tamis de 25 μm, pour lequel on ne considérera que tous les éléments mesurent moins de 25 μm. La diffraction laser établirait que ces « cylindres » sont différents, car ils présentent des valeurs différentes.
| Taille du cylindre | Rapport géométrique | Diamètre sphérique équivalent | |
|---|---|---|---|
| Hauteur | Diam. | ||
| 20 | 20 | 1:1 | 22,9 |
| 40 | 20 | 2:1 | 28,8 |
| 100 | 20 | 5:1 | 39,1 |
| 200 | 20 | 10:1 | 49,3 |
| 400 | 20 | 20:1 | 62,1 |
| 10 | 20 | 0,5:1 | 18,2 |
| 4 | 20 | 0,2:1 | 13,4 |
| 2 | 20 | 0,1:1 | 10,6 |
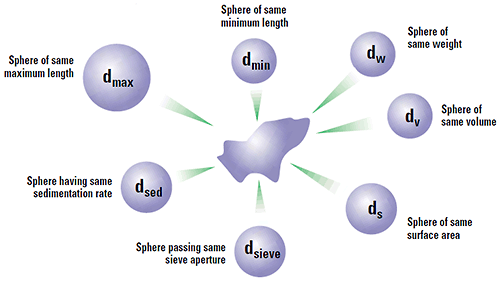
Il est évident qu'en observant notre particule au microscope, nous étudions sa projection en 2D et que nous pouvons mesurer un certain nombre de diamètres pour caractériser la particule. En utilisant la longueur maximale de la particule comme taille de référence, nous considérons que notre particule est une sphère dont cette valeur correspond à la dimension maximale. De même, en utilisant le diamètre minimal ou une autre valeur comme le diamètre de Feret, nous obtiendrons une autre réponse concernant la taille de la particule. Il convient donc d'avoir conscience que chaque technique de caractérisation mesurera une propriété particulière de la particule (taille maximale, taille minimale, volume, surface, etc.) et donc que nous obtiendrons une réponse distincte par rapport à une technique différente mesurant une autre dimension. La Figure 3 indique différentes réponses possibles pour un grain de sable. Aucune de ces techniques n'est fausse ; elles sont même toutes correctes. Les distinctions proviennent du fait qu'une propriété différente de la particule est mesurée à chaque fois. C'est comme si vous mesuriez votre boîte d'allumettes avec une règle graduée en centimètres, tandis que j'utilise une règle en pouces (et que vous mesurez la longueur, tandis que j'ai choisi la largeur !). Nous ne pouvons donc comparer de manière rigoureuse que les mesures effectuées sur une poudre à l'aide de la même technique.
|
Cela signifie également qu'il est impossible d'obtenir un standard de taille des particules pour des éléments tels que des grains de sable. Les standards doivent être sphériques pour permettre les comparaisons entre différentes techniques. Nous pouvons cependant utiliser un standard de taille de particule pour une certaine technique, ce qui permettra les comparaisons entre instruments utilisant cette technique.
Imaginons trois sphères de diamètre de 1, 2, 3 unités. Quelle est la taille moyenne de ces trois sphères ? De prime abord, on pourrait répondre 2,00. Comment avons-nous obtenu ce résultat ? Nous avons ajouté tous les diamètres
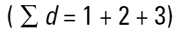
|
et les avons divisés par le nombre de particules (n=3). Il s'agit d'une moyenne en nombre (ou plus précisément d'une moyenne en longueur - nombre), dans la mesure où le nombre de particules figure dans l'équation :
Diamètre moyen =
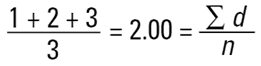
|
En mathématiques, cette valeur est appelée D[1,0], car les termes en haut de l'équation sont à la puissance (d1) et il n'y a pas de termes de diamètre (d0 ) en bas de l'équation. Cependant, imaginons que je suis ingénieur en catalyse. Je dois comparer ces sphères sur la base de la surface, car plus la surface est grande, plus l'activité du catalyseur est élevée. La surface d'une sphère est de 4πr2. Par conséquent, pour effectuer une comparaison basée sur la surface, nous devons élever les diamètres au carrée, diviser par le nombre de particules et calculer la racine carré pour revenir à un diamètre moyen :
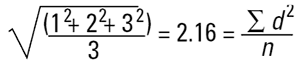
|
Il s'agit à nouveau d'une moyenne en nombre (moyenne nombre-surface), car le nombre de particules figure en bas de l'équation. Nous avons ajouté les carrés du diamètre, ce que nous appelons D[2,0] - termes de diamètre au carré au sommet, aucun terme de diamètre en bas.
Un ingénieur chimiste doit comparer les sphères en fonction de leur masse. N'oublions pas que la masse d'une sphère s'exprime comme suit :
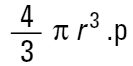
|
Nous devons cuber les diamètres, diviser par le nombre de particules et calculer la racine cubique pour revenir à un diamètre moyen :
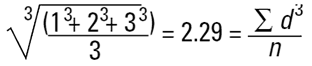
|
Il s'agit à nouveau d'un nombre moyen (moyenne nombre-volume ou nombre-masse), car le nombre de particules figure dans l'équation. En termes mathématiques, nous désignerons cette valeur D[3,0].
Le problème principal concernant la moyenne simple D[1,0], D[2,0], D[3,0], est que le nombre de particules est inhérent à la formule. Cela nous oblige à compter les particules lorsqu'elles sont nombreuses. Normalement, la numération des particules ne s'effectue que quand les nombres sont très bas (dans les ordres de grandeur ppm ou ppb), pour des applications telles que la contamination, le contrôle et le nettoyage. Un simple calcul indique que dans 1 g de silice (densité : 2,5), on aurait 760 x 109 particules si elles mesuraient toutes 1 μm.
C'est pourquoi il faut introduire le concept de moments calculés sur la distribution et, donc, de diamètre moyen. Les deux diamètres moyens les plus importants sont les suivants :
Ces moyennes sont similaires aux moments d'inertie et font entrer un autre terme linéaire dans le diamètre (la surface a une dépendance d3 et le volume ou la masse a une dépendance d4, comme indiqué ci-dessous) :
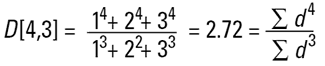
|
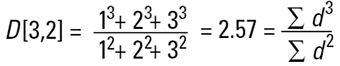
|
Ces formules indiquent le point central de la fréquence autour duquel aurait lieu la rotation de la distribution (surface ou volume/masse). Il s'agit en fait de centres de gravité des distributions respectives. L'avantage de cette méthode de calcul est évident : les formules n'incluent pas le nombre de particules. Par conséquent, les calculs des moyennes et distributions ne nécessitent pas de connaissance du nombre de particules concernées. La diffraction laser calcule initialement la distribution à partir des termes du volume, ce qui explique la représentation marquante de D[4,3].
En utilisant un microscope électronique pour mesurer nos particules, nous pourrions probablement obtenir leur diamètre à l'aide d'un graticule, avant de les ajouter et les diviser par le nombre de particules pour obtenir une moyenne. Nous pouvons obtenir la moyenne nombre-longueur D[1,0] à l'aide de cette technique. À l'aide d'une méthode d'analyse des images, nous pouvons mesurer la surface de chaque particule et diviser le résultat par le nombre de particules afin d'obtenir la valeur D[2,0]. En utilisant une méthode telle que la détection électrozone, nous pouvons mesurer le volume de chaque particule et diviser le résultat par le nombre de particules pour obtenir D[3,0].
La diffraction laser permet d'obtenir D[4,3] ou une moyenne de volume équivalente. Ce chiffre est identique à la moyenne de masse équivalente si la densité est constante.
Chaque technique aura donc tendance à générer un diamètre moyen différent et à mesurer différentes propriétés de notre particule. Rien d'étonnant à ce que la confusion règne parfois ! Par ailleurs, il existe une infinité de « bonnes » réponses. Imaginons trois sphères de diamètre de 1, 2, 3 unités :
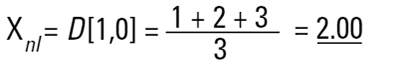
|
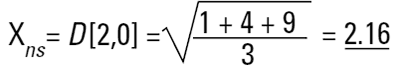
|
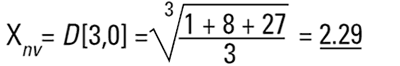
|
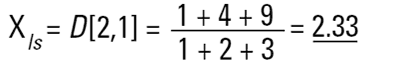
|
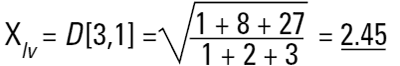
|
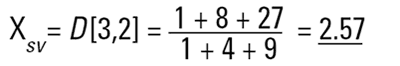
|
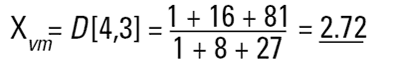
|
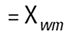
|
| Taille (cm) | Nombre d'objets | % par nombre | % par masse |
|---|---|---|---|
| 10-1000 | 7000 | 0,2 | 99,96 |
| 1-10 | 17500 | 0,5 | 0,03 |
| 0,1-1,0 | 3500000 | 99,3 | 0,01 |
| Total | 3524500 | 100,00 | 100,00 |
L'exemple ci-dessus est adapté d'un article paru dans la revue New Scientist (13 octobre 1991). Les scientifiques surveillent régulièrement les nombreux objets envoyés par l'homme dans l'espace, en orbite autour de la Terre. Les scientifiques les ont classés dans des groupes en fonction de leur taille.
En étudiant la troisième colonne ci-dessus, on peut conclure avec raison que 99,3 % de l'ensemble des particules sont extrêmement petites. Cette observation est une évaluation des données sur la base des NOMBRES. Cependant, en examinant la quatrième colonne, on pourrait déduire (avec raison) que la taille de pratiquement tous les objets est comprise entre 10 et 1000 cm. L'intégralité de la MASSE de l'objet se situe à cet endroit. Remarque : les distributions en NOMBRE et en MASSE sont très différentes et nous obtiendrions des conclusions très distinctes selon le type de distribution utilisé.
Aucune de ces distributions n'est fausse. Les données sont simplement examinées de manière différente. Par exemple, si nous étions en train de créer une combinaison spatiale, nous pourrions affirmer qu'il est facile d'éviter les 7 000 gros objets, ce qui couvre 99,96 % des cas. Cependant, le facteur le plus important concernant une combinaison spatiale concerne la protection contre les petites particules, dont le nombre représente 99,3 % !
En calculant les moyennes des distributions mentionnées ci-dessus, on pourrait constater que la moyenne en nombre est d'environ 1,6 cm et la moyenne en masse est de 500 cm. Une fois de plus, les résultats sont très différents.
En mesurant les particules à l'aide d'un microscope électronique, nous savons comme l'énonce une section précédente (« Différentes techniques permettent d'obtenir différentes moyennes. ») que nous calculons la valeur D[1,0] ou la taille moyenne nombre-longueur. Si nous recherchons spécifiquement la moyenne de taille en masse ou en volume, nous devons convertir notre moyenne en nombre pour obtenir une moyenne en masse. Sur le plan mathématique, cette opération est facile, mais penchons-nous sur les conséquences de ce type de conversion.
Imaginons que notre technique de mesure électronique est soumise à une marge d'erreur de ±3 % concernant la taille moyenne. En convertissant la taille moyenne en nombre pour obtenir une taille moyenne en masse, dans la mesure où la moyenne en masse est une fonction cubique du diamètre, nos erreurs seront cubées, c'est-à-dire qu'elles représentent une variation de ±27 % sur le résultat final.
Cependant, en calculant la distribution en masse ou en volume comme avec la diffraction laser, la situation n'est plus la même. Pour un échantillon stable mesuré dans des conditions de recirculation en suspension liquide, nous devrions pouvoir générer une reproductibilité de moyenne en volume de l'ordre de ±0,5 %. En convertissant cette moyenne en volume pour obtenir une moyenne en nombre, l'erreur ou la moyenne en nombre est la racine cubique de 0,5 %, soit moins de 1,0 % !
Sur le plan pratique, cela signifie qu'en utilisant un microscope électronique pour obtenir une distribution en volume ou en masse, l'effet produit en omettant ou en ne remarquant pas une particule de 10 μ est identique à ce qui se passerait en omettant ou en ne remarquant pas mille particules de 1 μ. Il est donc nécessaire d'avoir conscience des grands risques liés à l'interconversion.
Dans les granulomètres Malvern, les logiciels DOS™ et Windows™ calculent d'autres diamètres dérivés, mais il convient d'interpréter ces diamètres dérivés avec prudence. Il est possible de convertir différentes moyennes à l'aide des équations suivantes (transformation de Hatch-Choate) (Réf.7) :
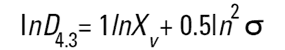
|
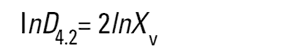
|
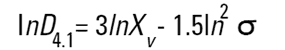
|
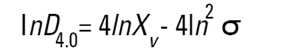
|
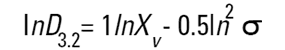
|
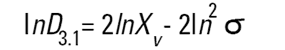
|
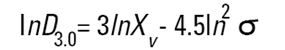
|
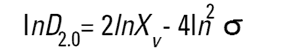
|
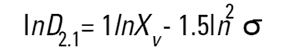
|
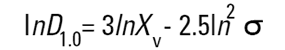
|
Nous avons vu que la technique de diffraction laser de Malvern Panalytical génère une distribution de volume pour les données d'analyse de l'énergie lumineuse (remarque : avec l'analyse de Fraunhofer, la distribution de surface projetée est supposée). Cette distribution en volume peut être convertie en tout diamètre de nombre ou de longueur, comme nous l'avons expliqué ci-dessus.
Cependant, dans toute technique d'analyse, il importe d'avoir conscience des conséquences de ce type de conversion (voir la section précédente intitulée « Interconversion entre les moyennes en nombre, longueur et volume/masse. ») et de savoir quel diamètre moyen est mesuré par l'équipement et quels diamètres sont véritablement calculés ou dérivés de ce premier diamètre mesuré.
D'autres techniques génèrent d'autres diamètres à partir de certains diamètres mesurés. Par exemple, un microscope mesure la valeur D[1,0] et peut dériver d'autres diamètres à partir de cette valeur.
Les diamètres mesurés sont plus fiables que les diamètres dérivés. En réalité, dans certains cas, il peut s'avérer très dangereux de s'appuyer sur une propriété dérivée. Ainsi, le tableau d'analyse de Malvern Panalytical nous donne une surface spécifique en m2/cc ou en m2/gm. Il ne faudrait pas prendre cette valeur au pied de la lettre. En fait, quand on cherche à obtenir la surface spécifique de notre matériau, il serait judicieux d'utiliser une technique spécifiquement conçue pour calculer la surface, telle que la théorie B.E.T. ou la porosimétrie au mercure.
Étant donné que chaque technique mesure une propriété ou une taille différente sur notre particule et qu'il existe plusieurs façons d'utiliser les données pour obtenir un diamètre moyen différent (D[4,3], D[3,2], etc.), quel nombre faut-il utiliser ? Prenons un exemple simple : deux sphères de diamètre de 1 et 10 unités. Imaginons que nous sommes en train de fabriquer de l'or. En calculant le diamètre moyen à l'aide d'un nombre simple, nous obtiendrons le résultat suivant :
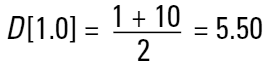
|
Nous pourrions supposer que la taille moyenne des particules du système est de 5,50 unités. Cependant, n'oublions pas qu'en fabriquant de l'or, c'est le poids du matériau qui nous intéresse.
C'est pourquoi il nous importe peu de savoir que le procédé génère 3,5 millions de particules. Nous voulons plutôt savoir que nous avons obtenu 1 kg ou 2 kg d'or.
Sachant que la moyenne en masse est une fonction cubique du diamètre, nous voyons que le diamètre d'une unité présente une masse d'une unité et que la sphère du diamètre de 10 unités possède une masse de 103 = 1000 unités.
En d'autres termes, la sphère la plus grosse représente 1000/1001 parties de la masse totale du système. Si nous fabriquons de l'or, nous pouvons nous débarrasser de la sphère d'une unité, car cela en représente une perte de moins de 0,1 % de la masse totale du système. Par conséquent, la moyenne en nombre ne reflète pas fidèlement la répartition physique de la masse. C'est dans ce type de situation que D[4,3] s'avère particulièrement utile.
Dans l'exemple de nos deux sphères, on pourrait calculer le diamètre moyen en masse ou en volume comme suit :
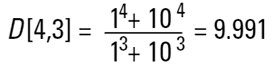
|
Cette valeur nous indique plus précisément où se situe la masse du système, ce qui s'avère plus utile pour les ingénieurs en chimie.
Cependant, imaginons que nous fabriquons des plaques de silicone ou d'arséniure de gallium dans une salle propre. La chute d'une particule sur la plaque produit en général un défaut. Dans cette situation, le nombre ou la concentration des particules revêt une immense importance, car une particule équivaut à un défaut. Nous devons alors utiliser une technique mesurant directement le nombre de particules ou indiquant la concentration de particules. Il s'agit essentiellement de la différence entre le dénombrement des particules et la granulométrie laser. Le dénombrement compte toutes les particules. La taille a moins d'importance et nous n'avons besoin que d'un nombre limité de classes granulométriques (disons, 8). Dans le cadre de la granulométrie, le nombre absolu de particules est moins important que les tailles ou la distribution granulométrique des particules, ce qui nous obligera éventuellement à utiliser plus de classes granulométriques.
Pour un inhalateur à dose destiné aux asthmatiques, la concentration du médicament est aussi importante que sa distribution granulométrique.
Il est important de définir ces trois termes, car ils sont souvent utilisés à mauvais escient, aussi bien dans le domaine des statistiques que de l'analyse de la taille des particules :
Cela correspond à la moyenne arithmétique des données. Divers types de moyennes peuvent être calculées pour les particules (voir la section D[4,3] etc.).
Il s'agit de la valeur de la taille des particules, qui divise la population en deux parties égales. En d'autres termes, 50 % de la distribution se situe au-dessus de cette valeur et 50 % en dessous.
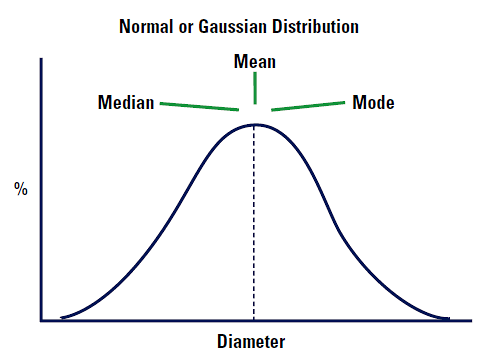
Il s'agit de la valeur la plus courante de la distribution en fréquence, c'est-à-dire du point culminant de la courbe en fréquence.
|
Imaginons que notre distribution est une distribution normale ou gaussienne. La moyenne, la médiane et le mode se situeront exactement aux mêmes endroits. Voir la Figure 4.
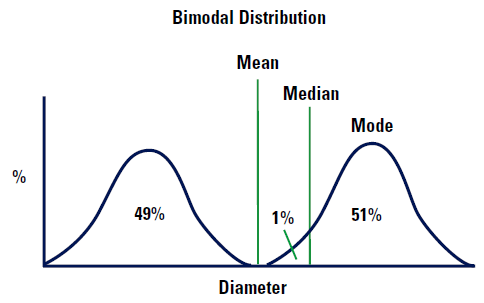
Imaginons que notre distribution est bimodale, comme l'illustre la Figure 5.
|
Le diamètre moyen se situera presque exactement entre les deux distributions, comme nous l'illustrons. Remarque : il n'existe aucune particule de cette taille moyenne ! Le diamètre médian se situera à 1 % dans la plus haute des deux distributions, car il s'agit du point qui scinde la distribution en deux parts égales. Le mode se situe au sommet de la courbe supérieure, car il s'agit (tout juste) de la valeur la plus fréquente pour le diamètre.
Cet exemple prouve qu'il n'y a aucune raison pour que la moyenne, la médiane et le mode soient identiques ou même similaires. Tout dépend de la symétrie de la distribution.
Remarque : dans le tableau d'analyse de Malvern Panalytical :
Dans les sections précédentes, nous avons vu que chaque technique de mesure produisait une réponse différente, car elle mesure une dimension différente de la particule. Nous allons maintenant aborder certains avantages et inconvénients des principales méthodes employées.
Cette très vieille technique présente l'avantage d'un faible coût et d'une disponibilité immédiate pour de grosses particules, comme celles qu'on trouve dans le secteur minier. Terence Allen (Réf. 2) a abordé les difficultés d'un tamisage reproductible. Ses inconvénients principaux pour la plupart des utilisateurs sont les suivants :
Cette méthode traditionnelle de granulométrie dans les secteurs de la peinture et la céramique est séduisante car elle permet d'obtenir des diamètres très petits ! La plage concernée est de 2 à 50 microns (Réf. 1 & 2), malgré les affirmations des fabricants.
Le principe de mesure s'appuie sur l'équation de Stokes :
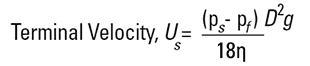
|
L'équipement utilisé peut aller du plus simple, comme une pipette d'Andreason, au plus compliqué, comme les systèmes mettant en œuvre des disques centrifuges ou des rayons X.
L'étude de cette équation révèle quelques écueils potentiels. Il faut connaître la densité du matériau, ce qui rend cette méthode impossible à utiliser pour les émulsions, puisque le produit ne subit pas de sédimentation, ou pour les matériaux très denses pour lesquels la sédimentation se produit rapidement. On finit par obtenir un diamètre de Stokes (DST), qui diffère du diamètre pondéré en masse D[4,3] et qui compare simplement le taux de sédimentation de la particule au taux similaire de sédimentation d'une sphère. Le terme de viscosité dans le dénominateur indique que la température nécessite un contrôle précis. Un changement de 1°C pour la température induit un changement de 2 % de la viscosité.
L'équation permet de calculer relativement facilement le temps de sédimentation. On peut démontrer que la sédimentation d'une particule de SiO2 d'un micron (ρ = 2,5) prendra 3,5 heures sur 1 cm sous l'effet de la gravité, dans une eau à 20°C. Les mesures sont donc extrêmement lentes et leur répétition très rébarbative. L'une des solutions pour contourner ce problème consiste à augmenter la gravité.
Nous abordons les inconvénients d'une augmentation de la gravité en (Réf. 3). Vous trouverez des critiques plus approfondies de la technique de sédimentation en (Réf. 2).
La loi de Stokes ne s'applique qu'aux sphères, qui possèdent la caractéristique unique de présenter la forme la plus compacte pour leur volume ou surface. C'est pourquoi des particules « normales » aux formes plus irrégulières présentent une surface supérieure à une sphère, et chutent donc plus lentement, en raison de la résistance accrue par rapport à leur diamètre de sphère équivalente.
| Déplacement en 1,0 seconde (μm) | ||||||
|---|---|---|---|---|---|---|
| Dans l'air à 70°F (1 atm) | Dans l'eau à 70°F | Dans l'eau à 70°F | ||||
| Diamètre des particules (µm) | Dû au mouvement brownien* | Dû à la sédimentation gravitationnelle+ | Dû au mouvement brownien* | Dû à la sédimentation gravitationnelle+ | Y | k=100Y(%) |
| 0,10 | 29,4 | 1,73 | 2,36 | 0,005 | 31,1 | 96,9 |
| 0,25 | 14,2 | 6,3 | 1,49 | 0,0346 | 3,15 | 75,9 |
| 0,50 | 8,92 | 19,9 | 1,052 | 0,1384 | 0,556 | 35,7 |
| 1,0 | 5,91 | 69,6 | 0,745 | 0,554 | 0,0983 | 5,0 |
| 2,5 | 3,58 | 400 | 0,334 | 13,84 | 0,00995 | 1,0 |
| 10,0 | 1,75 | 1550 | 0,236 | 55,4 | 0,00031 | 0,03 |
*Déplacement moyen obtenu par équation (7.20)
+Distance de sédimentation pour une sphère d'une densité de 2000 kg/m3, en tenant compte de la correction de Cunningham.
Y est défini dans l'équation (7.23) (grâce à la Référence 2, p. 259)
Pour des objets en forme de disque, tels que les kaolins, cet effet est encore plus accentué et des déviations plus marquées sont à prévoir.
Par ailleurs, en ce qui concerne les petites particules, deux processus contraires s'opèrent : sédimentation gravitationnelle et mouvement brownien. La loi de Stokes ne s'applique qu'à la sédimentation gravitationnelle. Le tableau en sommet de page illustre un comparatif des deux processus opposés. Il permet de confirmer que de grosses erreurs (près de 20 %) se produiront si la sédimentation est utilisée pour des particules de moins de 2 μm, tandis que les erreurs dépasseront 100 % pour les particules de 0,5 μm.
La technique de sédimentation permet d'obtenir un résultat inférieur aux données réelles, ce qui explique pourquoi certains fabricants se fourvoient. Pour conclure, les principaux inconvénients de cette technique pour les utilisateurs de pigments sont les suivants :
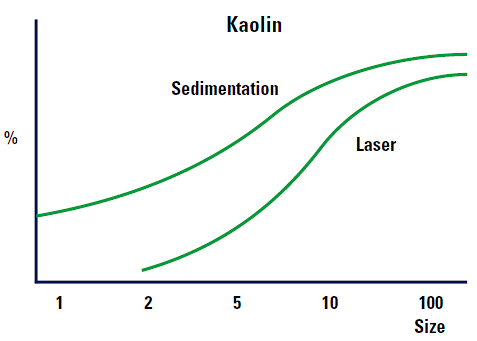
La Figure 6 illustre les différences prévues dans les résultats par sédimentation et par diffraction laser.
|
Cette technique a été développée au milieu des années 50 pour mesurer la taille des cellules sanguines qui sont en suspension dans un électrolyte dilué et de taille quasiment monomodale.
Le principe de fonctionnement est très simple. Un orifice est pratiqué dans un récipient en verre. Le liquide en suspension diluée passe dans cet orifice et un courant est appliqué. Tandis que les particules passent dans l'orifice, la capacité électrique change, ce que confirme une impulsion ou un pic de tension. Dans les instruments les plus anciens, les pics de taille étaient mesurés et comparés au pic de taille d'un standard de latex. Cette méthode n'est donc pas absolue, mais comparative. Les problèmes d'orientation des particules peuvent être corrigés en effectuant les mesures sous le pic, plutôt qu'au niveau du pic. Pour les cellules sanguines, la technique est sans égale. Cette méthode permet d'obtenir aussi bien un nombre de particules qu'une distribution en volume. Pour les matériaux industriels réels, tels que les pigments, cette méthode présente certains inconvénients :
Cette technique est donc parfaite pour les cellules sanguines, mais donne de moins bons résultats pour de nombreux matériaux industriels.
Cette technique est excellente, car elle permet d'observer directement les particules. Avec cette méthode, on peut observer la forme des particules et évaluer si la dispersion s'est effectuée de manière adéquate ou si une agglomération s'est produite dans le système. Cette méthode est relativement bon marché et avec certains microscopes, il est possible d'utiliser une analyse d'images pour obtenir des valeurs (habituellement 6 ou 8 chiffres après la virgule, ce qui dépasse largement la résolution de la technique !).
Il est intéressant de remarquer que 1 g de particules de 10 μm (densité de 2,5) contient 760 x 106 particules. Il serait impossible de les examiner individuellement au microscope.
Cependant, cette technique n'est pas adéquate dans l'optique d'un contrôle qualité ou de production, au-delà d'une simple évaluation, comme expliqué ci-dessus. Le nombre de particules examinées est relativement bas et il existe un réel danger d'obtenir un échantillonnage non représentatif. Par ailleurs, en cas de mesure de la distribution de masse, les erreurs sont amplifiées : manquer ou omettre une particule de 10 μm revient à négliger mille particules de 1 μm.
La microscopie électronique nécessite une préparation d'échantillons élaborée et s'avère lente. La microscopie manuelle ne permet d'examiner qu'un nombre restreint de particules (au plus 2 000 par jour pour un utilisateur chevronné) et la fatigue s'instaure rapidement chez l'utilisateur. Le problème de la dimension mesurée se pose également, ce qui peut donner lieu à d'immenses variations d'un opérateur à l'autre sur le même échantillon. Utilisée de concert avec la microscopie par diffraction, elle peut s'avérer très utile dans la caractérisation des particules.
Il serait plus rigoureux de parler de diffusion de la lumière laser à petit angle (LALLS). Cette méthode est devenue la technique préférée dans de nombreux secteurs d'activité en matière de caractérisation et de contrôle qualité. Conformément à la norme ISO13320, la plage d'application va de 0,1 à 3000 μm. L'instrumentation de ce secteur a fait l'objet de développements continus depuis une vingtaine d'années. Cette méthode s'appuie sur le fait que l'angle de diffraction est inversement proportionnel à la taille des particules. Les instruments utilisés sont :
Certains instruments plus anciens, ainsi que quelques modèles récents, s'appuient sur l'approximation de Fraunhofer, qui suppose les éléments suivants :
Ces suppositions ne sont jamais exactes pour de nombreux matériaux et peuvent induire des erreurs approchant 30 %, notamment quand l'indice relatif de réfraction du matériau et du milieu approche de l'unité. Quand la taille de la particule est proche de la longueur d'onde de la lumière, la diffusion devient une fonction complexe accompagnée de valeurs minimales et maximales. Les instruments les plus récents (tels que le Mastersizer 2000 de Malvern Instruments) reposent sur la théorie complète de Mie, qui résout intégralement les équations d'interaction entre la lumière et la matière. Cela permet d'obtenir des résultats très précis sur une large plage de tailles (0,02 -2000 μm, habituellement). La théorie de Mie s'appuie sur une supposition du volume de la particule, contrairement à Fraunhofer qui correspond à une prédiction de la surface prévue.
La « pénalité » de cette précision totale réside dans le fait qu'il faille savoir les indices de réfraction du matériau et du milieu, et connaître ou supposer le facteur d'absorption de l'indice de réfraction. Cependant, pour la majorité des utilisateurs, cet impératif ne présentera aucun problème, puisque ces valeurs sont généralement connues ou peuvent être mesurées.
La diffraction laser confère les avantages suivants à l'utilisateur :
1. Paint and Surface coatings - theory and practice; Ed. R. Lambourne Ellis Horwood Ltd. 1993. ISBN 0-13-030974-5PGk
2. Particle Size Measurement;T. Allen, Chapman & Hall. 4th Edition, 1992. ISBN 04123570
3. G.J.J.Beckers, H.J.Veringa; Powder Technology 60 (1989) p245-248.
4. J. Ranucci Pharmaceutical Technology; October 1992 pp 108-114.
5. G. Hind; Manufacturing Chemist August 1990 pp 28-30.
6. M.W.Wedd; ILASS-Europe 8e conférence annuelle, Koninklijke/Shell Laboratorium, Amsterdam 30 septembre -2 octobre 1992.
7. T. Hatch & S.P Choate. J. Franklin Inst. 207 pp 369-387 (1929).