Static light scattering is a technique to measure the molecular weight using the relationship between the intensity of light scattered by a molecule and its molecular weight and size. These relationships are described by Rayleigh theory which states that the molecular weight of a molecule is proportional to the Rayleigh ratio of scattered light i.e. the ratio of scattered light intensity to incident light intensity.
All static light scattering instruments detect the amount of light scattered by a sample to measure its molecular weight; however, as molecules grow in size, a second factor called angular dependence becomes significant. Angular dependence affects the intensity of scattered light and hence the calculated molecular weight. It must therefore be accounted for.
| GPC | Gel permeation chromatography |
| SEC | Size exclusion chromatography |
| LALS | Low angle light scattering |
| RALS | Right angle light scattering (90° light scattering) |
| MALS | Multi angle light scattering |
| SLS | Static light scattering |
| DLS | Dynamic light scattering |
| Rg | Radius of gyration |
| RH | Hydrodynamic radius |
| MW | Molecular weight (Molar Mass) |
| Mn | Number-average molecular weight |
| Mw | Weight-average molecular weight |
| Mz | Z-average molecular weight |
| A2 | Second virial coefficient (B22) |
Light scattering can be a confusing topic. There are a number of different techniques that come under the general heading of light scattering and a range of parameters that can be measured. The lines between these can become blurred, as some systems use more than one technique in a single instrument, so it is very easy to lose sight of the most important factors when considering which light scattering technology is right for your application.
Static light scattering, also called classical light scattering, is a technique used to measure molecular weight and molecular radius of gyration. Within static light scattering, there are a number of different technologies with acronyms such as SLS, MALS, LALS and RALS and others. Each of these is subtly different and each has advantages and disadvantages.
This white paper describes, in some detail, the principles and theories behind static light scattering. The theory, technique and the different technologies are described and compared. By reading this white paper, you should be able to understand the background to these measurements and make an informed choice on the most appropriate solution for your application.
Each section provides a great deal of detail, but begins with a few key points to summarise the information contained so you can decide whether you need to read the detail in that section.
Molecular weight is a property that describes the mass of an individual molecule. Scientifically, it is the mass of a material required to make 1 mole of the sample. For example, carbon has a molecular weight 12 g/mol. The units of molecular weight are grams per mole (g/mol). However these are often referred to as Daltons (Da), or sometimes more conveniently kilo Daltons (kDa)
For a pure protein sample, it is expected that it would have a fixed molecular weight and that all of the protein molecules within the sample should have the same molecular weight. For a natural or synthetic polymer sample, the molecular weight of the molecules within a particular sample will have a distribution that could have many forms. The term that describes the overall width of the distribution is 'polydispersity'. A sample with a very narrow range of molecular weights is said to have a low polydispersity or to be very monodisperse. A sample with a wider range of molecular weights is said to have a high polydispersity.
The majority of samples contain a range of molecular weights, particularly natural and synthetic polymers. These distributions of molecular weights can be described in a number of ways, and one common way is to use the molecular weight moments Mn, Mw and Mz, which are the number-averaged, weight-averaged and z-averaged molecular weights respectively. These are defined by equations shown below, where ci and Mi are the concentration and molecular weight at each data slice:

|

|

|
Intuitively, the number-averaged molecular weight is the total mass of material divided by the total number of molecules and is therefore a numerical average. It is weighted towards the lower mass molecules which will be more numerous. Properties such as vapour pressure lowering, freezing point depression and osmotic pressure depend on the number of molecules and not on their size. The weight average molecular weight is calculated by multiplying by the molecules mass, so the average is biased towards the larger molecules in the distribution. Properties like diffusion, sedimentation, light scattering depend both on the size and the mass of the molecules. The z-average molecular weight includes a further multiplication of the molecules' molecular weight. It is therefore heavily weighted to the largest molecules in the sample and can be determined directly by the ultracentrifugation technique.
Using these three values, it is possible to get an idea of the entire molecular weight distribution. Clearly, the closer these values are to each other, the lower the polydispersity and the further apart they are, the higher the polydispersity. Polydispersity is defined according to the equation
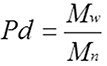
|
Since Mw is always equal to or larger than Mn, the lowest possible value for polydispersity (Pd) is 1 but there is no theoretical upper limit. Natural and synthetic polymers have a wide range of polydispersities but since proteins have fixed molecular weights, we can expect the polydispersity of a protein to be very low (close to 1) for well-behaved proteins.
Molecular size is the physical size of a molecule. Typically, a single value is used to describe the size. This value is the radius of a sphere of an equivalent size to the molecule being measured. The two most commonly used values of molecular size are RH (hydrodynamic radius) and Rg (radius of gyration). The hydrodynamic radius is the radius of an equivalent sphere that diffuses at the same speed as the molecule under study. It is calculated either from dynamic light scattering or from intrinsic viscosity and so will not be considered further here. (For more information on hydrodynamic radius see the technical notes, "Dynamic Light Scattering: An Introduction in 30 Minutes" and "Protein and polymer molecular size by GPC/SEC", on the Malvern website).
The radius of gyration is the root-mean-square of the radii from the centre of mass to the different mass cores within the molecule. It is sometimes called Rrms (root-mean-square). The units for a molecular size are nanometers (nm). Rg is calculated using static light scattering so will be considered in more detail later in the document.
When a photon collides with a molecule, some of the energy from the photon is used to initiate what is called an oscillating dipole within the molecule. This energy is subsequently re-emitted by the molecule in all directions as light. We see this phenomenon every day in white clouds, sunsets or in dust passing through a beam of sunlight or light from a projector. The principles behind light scattering can be used to measure a number of properties related to the molecule.
The properties of the light scattered by molecules and particles vary depending on the object doing the scattering as defined in the Rayleigh equation.

|
Where:

|
Where:

|
Where:
In simpler terms, the Rayleigh equation tells us that the intensity of scattered light at a given angle is dependent on a number of factors including both molecular weight and molecular size of the sample under study. As can be seen in the Rayleigh equation, molecules with higher molecular weight and larger sizes will scatter more light. While the increase in the intensity of light scattered is linear with molecular weight, it is non-linear with respect to size.
So, if we know all of the other factors in the Rayleigh equation, we can measure the intensity of the scattered light (related to Rθ) and calculate the sample's molecular weight.
Static light scattering (SLS) uses an optical arrangement such that the signal detected is 'static' or stable. By measuring the intensity of light scattered by a sample in situations where the other constants are known, the molecular weight of the sample can be calculated.
The term static light scattering is used to differentiate the technique from dynamic light scattering which is a separate, though not unrelated, technique for measuring particle size. For more information on dynamic light scattering, see the Malvern technical note "Dynamic Light Scattering: An Introduction in 30 Minutes" or the 'inform' white paper "A basic guide to particle characterization" on the Malvern website.
Static light scattering measurements can be made in a cuvette or in a gel-permeation chromatography (GPC)/size-exclusion chromatography system (SEC). Using a chromatography system removes a number of problems to do with preparing and purifying the sample and so is the most common implementation of SLS. Additionally, GPC/SEC allows us to easily combine the light scattering data with data from a concentration detector to measure the sample's concentration at the same time and thus use both sets of information in our calculations. The most common concentration detector is a refractive index detector (RI) but an ultraviolet (UV) absorbance detector can also be used.

|
The Rayleigh equation shown previously includes the term 1/Pθ, which so far we have assumed we know the values for. However, this is actually not true and it is here that all of the differences between different light scattering instruments come into play.
Pθ, or form factor, is related to the size of the molecule and the angle at which the scattering is determined. This term is defined as:

|
Where:
It can be seen from the equation that 1/Pθ is dependent on a number of factors to do with both the sample and the measurement. These include the solvent refractive index (n0), the laser wavelength in a vacuum (λo), the measurement angle (θ) and the size of the molecule we are measuring (Rg).
This means that for larger molecules, the amount of light scattered will depend on the measurement angle. This is called 'angular dependence' and the reason for this phenomenon is that as the molecular size increases the scattered photons no longer scatter independently, but constructively and destructively interfere with each other as shown in the figure 2.

|
When the molecule is small with respect to the laser, as in figure 2A, it acts as a point scatterer. In this situation the light is scattered by the molecule with even intensity in all directions. These molecules are called 'isotropic scatterers'.
However, as the molecule grows in size with respect to the laser, the molecule's size and structure starts to become important. Individual photons from the laser are scattered by different points within the molecule. This is dependent on Rg. These scattered photons vary in phase so will interfere with each other and the resulting measured intensity will depend on the observation position. These molecules are called 'anisotropic scatterers'. At the sizes we are interested in, all of the interference is destructive which means that the intensity will always appear to be lower than if we assumed it was an isotropic scatterer. If we were to use this intensity to calculate the molecular weight using the Rayleigh equation, we would therefore underestimate it.
In order to remove this effect, the Rayleigh equation tells us that if we were able to make a measurement of the intensity of the scattered light at a θ of 0°, then sin2(θ/2) would be 0 and 1/Pθ would be 1. So at 0° the intensity of scattered light would be unaffected by the interference and we could relate the intensity to the molecular weight in the same way we can with smaller molecules, measuring at a 90° angle. Unfortunately, we cannot do this as the intensity of the illuminating laser at 0° is so much stronger than the scattered light that we cannot separate out the purely scattered light. As we cannot measure directly at 0° we need to find an alternative technique.
The rule of thumb to use when deciding where angular dependence starts is to say that, at a diameter below 1/20th of the laser wavelength, molecules scatter isotropically, and above this level you have anisotropic scattering. Most instruments usually have lasers with wavelengths between 633 and 670 nm (red) so the limit of isotropic scattering is between 15.8 and 16.8 nm radius (Because of the dependence on laser wavelength, the same calculation for a laser with a wavelength of 532 nm (green) will give a value of 13 nm).
This nominal value of around 15 nm radius for the onset of measurable angular dependence will also be the lower limit at which you can still reliably measure the molecular size, Rg . (See "How do we get the molecular size, Rg, from the data?" below)
The different types of light scattering instrument are designed to overcome the angular dependence issue in different ways and these are described in the next section.
In order to overcome the angular dependence, we must decide what the intensity of the scattered light is at 0° based on data from other angles. The best way to calculate and represent this is in a 'Guinnier Plot', which is a simplification of a Zimm plot where the second virial coefficient is not required.
A Guinnier plot is a plot of KC/Rθ as a function of angle (sin2(θ/2)). Other plots and models are available but this is the most common. An example is shown in the figure 3.

|
Measurements of light scattering intensity are made at the desired angle. With knowledge of the sample's concentration and other factors,
KC/Rθ can then be calculated and is plotted in the graph as a function of sin2 (θ/2). The y-intercept (which equates to an angle of 0°) is 1/Mw from which the molecular weight can be calculated easily.
The initial slope of the line is:

|
Rg can then be calculated from this equation with relative ease. However, at small molecular sizes, the slope will be very small and hidden in the noise in the data. Only when the molecule gets to an appreciable size compared to the wavelength of the laser light will the slope be large enough to obtain a reliable Rg value. As described above, the nominal threshold for a 633nm laser is an Rg of ≈15 nm. However, the absolute limit for measuring Rg may be lower or higher than this nominal 15 nm, depending on the sample, solvent and the conditions of measurement. Many MALS instrument manufacturers put a limit of 10 nm (or even lower) on their instrument specifications. This is often for standard polymers of high dn/dc values and at high concentrations run under ideal conditions. In practice, this limit will not be achievable on all samples. At the other extreme, with samples of poor dn/dc run under non-ideal conditions, the smallest Rg that can be measured may be much higher than the nominal 15nm value.
There are 4 different types of SLS instruments available. RALS, LALS, Hybrid RALS/LALS and MALS.
A RALS device is the simplest light scattering instrument available. It measures the intensity of the light scattered at 90° to the incident beam as in figure 4A. The molecular weight of the sample is then calculated directly from the intensity measured and the sample concentration. In the Zimm plot in figure 4B the intensity of the scattered light is measured far from the y-axis and it is assumed that the sample scattering is isotropic (i.e. equal at all angles).

|
A RALS system has a number of advantages:
However, RALS detectors have some limitations:
Since proteins are almost always smaller than 15nm radius, and scatter light only weakly, they require a sensitive detector. Hence RALS detectors are excellent for measuring protein molecular weight.
A LALS detector measures the intensity of light scattered at an angle that is as close as possible to 0° as shown in figure 5A. This has the advantage that the intensity will be very close to the intensity at 0° and so the calculated molecular weight will be very close to the actual molecular weight of the molecule. To be considered a LALS detector, the angle must be less than 10° and the most common LALS detectors have a measurement angle of 7° but the closer the measurement to 0°, the more accurate the measurement will be. This will be true irrespective of the size of the molecule that we are measuring. Looking at the Zimm plot (figure 5B), a LALS measurement is very close to the axis and therefore very close to the y-intercept. This means that the error by measuring at 7° is very low. With a LALS measurement at 7°, sin2(θ/2) is just 0.0037, which equates to less than 1% error in the MW even for the largest molecules.

|
A LALS system has a number of advantages:
LALS detectors also have a number of limitations:
Overall, LALS measurements offer an accurate way to measure molecular weight using static light scattering. LALS is particularly useful for measuring the molecular weight of large anisotropic scatterers such as synthetic and natural polymers.
Based on the discussion above, it is clear that RALS and LALS detectors are complementary RALS detectors have the sensitivity to measure small isotropic scatterers and LALS detectors can measure the molecular weight of large molecules with unrivalled accuracy. A RALS/LALS hybrid therefore combines these two measurements into a single cell as shown in figure 6A. On the Zimm plot, the RALS detector is used to measure molecules whose size is below the ≈15 nm threshold of isotropic scattering. The LALS detector is used to accurately measure molecules whose size is above the ≈15 nm threshold of isotropic scattering. Software switches automatically from LALS to RALS according to the detector signals. For samples that scatter anisotropically, the ratio of the two calculated molecular weights can be used to estimate Pθ. This in turn can be used to estimate a value for Rg assuming a structural model such as a random coil or a hard sphere.

|
The RALS/LALS combination offers the advantages of both:
Limitations of the RALS/LALS hybrid include:
Overall, a RALS/LALS hybrid offers the advantages of RALS and LALS and suffers none of the drawbacks of either. This makes a RALS/LALS hybrid system excellent for measuring the molecular weight of any sample.
As the name suggests, MALS detectors measure the intensity of the scattered light at many angles as can be seen in figure 7A. By plotting these points on a Zimm plot (figure 7B), a best fit line can be extrapolated back to 0° from where the molecular weight can be calculated. The initial slope of this line enables an accurate calculation of molecular size, Rg.

|
MALS detectors have a number of their own advantages:
However, MALS systems also have some limitations:
When making measurements using MALS, the most important factor is that the form of the extrapolation is unknown and accurate fitting is particularly dependent on the number of low angles and the accuracy of the points. It is therefore important that a MALS instrument should have as many low angles as possible as this will provide the most accurate extrapolation back to 0°. In general, in order to maximise the accuracy of the extrapolation, having more angles is beneficial.
In summary, MALS offers a universal solution for measuring molecular weight and Rg of all different types of sample but the nature of the design forces some compromises on the measurement.
Light scattering techniques are often called 'absolute' but this is often misunderstood.
Although the column doesn't need calibrating, all light scattering devices require calibration in some form. The only question is how the device should be calibrated and this can be done in a number of ways:
The principle of light scattering calibration, as with all calibrations, is to reference the size of the response signal to the parameter being measured. In static light scattering, we relate the magnitude of the signal from the photo-detector to the intensity of the scattered light and then to the molecular weight of the sample. As well as all the sample dependent factors described in the Rayleigh equation, the measured intensity of the scattered light will depend on a large number of instrument dependent variables including:
It is not possible to characterise all of these components in a system to the accuracy required of the measurement; so instead they are all accounted for by a calibration step.
There are two methods by which a system can be calibrated but they are functionally identical.
The principle behind a molecular weight standard-based calibration is to run a sample of known molecular weight through the SLS detector while it is attached to a GPC/SEC system. The magnitude of the response of the light scattering detector and the known sample concentration, molecular weight and dn/dc are used to calculate an instrument response factor or calibration constant for the light scattering detector. Discounting other values such as the solvent refractive index and laser wavelength, the light scattering detector calibration constant is defined as:

|
Where:
With a standard, the concentration and injection volume (and therefore mass) are known, as is the standard molecular weight and dn/dc.
This allows the calibration constant to be calculated and can be performed on every angle in a light scattering detector simultaneously.
Once the calibration constant has been determined, the molecular weight for any sample can be measured:

|
Where:
Mw = the molecular weight of the sample,
δLS = measured intensity of light scattered by the sample,
dn/dc = is the sample refractive index increment,
mass = the injected mass of the sample,
kls = the light scattering calibration constant.
In a GPC/SEC system containing multiple detectors, all of them can be calibrated at the same time using a standard that is well characterised and traceable. A further benefit of calibrating the detectors in this way is that the inter-detector volumes between the different detector flow cells and the band broadening and tailing that occur as the sample travels between detectors can all be accounted for in the same step.
The final benefit of this method is that the system calibration can be checked and/or re-calibrated at any time by the user. This is particularly useful as instrument constants will drift over time due to a number of factors such as degradation of light sources, cleanliness of flow cells, changing detector tubing etc.
A molecular weight standard-based calibration therefore allows all of the instrument response factors/calibration constants to be derived at the same time as the inter-detector volumes and peak broadening parameters are all calculated. It offers the most effective way of calibrating a system and, by its very nature, it also offers a clear way to check the calibration of a system by comparing the responses of the standard to that at the time of calibration.
The principle behind a scattering standard-based calibration is to fill the light scattering flow cell with a solvent of known scattering such as toluene. Toluene has a well characterised Rayleigh ratio (the ratio of scattered light intensity to incident light intensity) so by measuring the scattering signal observed from toluene it is possible to calculate the scattering signal from the sample. Rθ for the sample is calculated according to the equation:
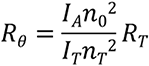
|
Where:
The sample molecular weight is then calculated by inputting this value of Rθ into the Rayleigh equation. This means that the calibration constant in this situation is essentially:

|
Although you do not need a molecular weight value to calibrate a detector, the principle of calibrating with a scattering standard is identical in that you are using a standard to measure the response of the light scattering detector to a known sample.
This method has a number of other significant drawbacks:
Overall then, a scattering standard-based calibration is a more labour intensive process that does not improve the calibration and only serves to add more hurdles to achieving an accurate calibration of a system.